Nearest Neighbor Dirichlet Process
Paper and Code
Mar 17, 2020
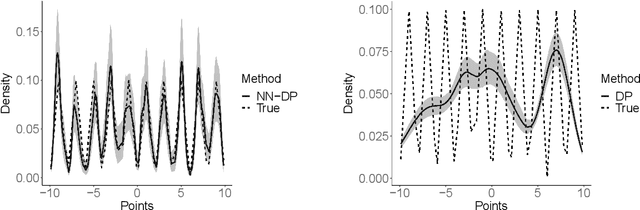
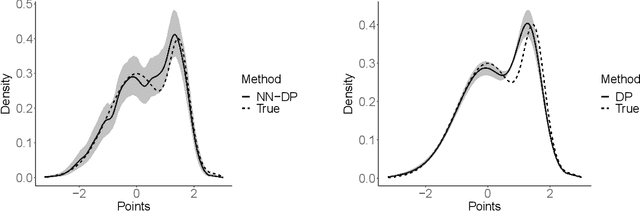

There is a rich literature on Bayesian nonparametric methods for unknown densities. The most popular approach relies on Dirichlet process mixture models. These models characterize the unknown density as a kernel convolution with an unknown almost surely discrete mixing measure, which is given a Dirichlet process prior. Such models are very flexible and have good performance in many settings, but posterior computation relies on Markov chain Monte Carlo algorithms that can be complex and inefficient. As a simple and general alternative, we propose a class of nearest neighbor-Dirichlet processes. The approach starts by grouping the data into neighborhoods based on standard algorithms. Within each neighborhood, the density is characterized via a Bayesian parametric model, such as a Gaussian with unknown parameters. Assigning a Dirichlet prior to the weights on these local kernels, we obtain a simple pseudo-posterior for the weights and kernel parameters. A simple and embarrassingly parallel Monte Carlo algorithm is proposed to sample from the resulting pseudo-posterior for the unknown density. Desirable asymptotic properties are shown, and the methods are evaluated in simulation studies and applied to a motivating dataset in the context of classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge