Empowering SMPC: Bridging the Gap Between Scalability, Memory Efficiency and Privacy in Neural Network Inference

This paper aims to develop an efficient open-source Secure Multi-Party Computation (SMPC) repository, that addresses the issue of practical and scalable implementation of SMPC protocol on machines with moderate computational resources, while aiming to reduce the execution time. We implement the ABY2.0 protocol for SMPC, providing developers with effective tools for building applications on the ABY 2.0 protocol. This article addresses the limitations of the C++ based MOTION2NX framework for secure neural network inference, including memory constraints and operation compatibility issues. Our enhancements include optimizing the memory usage, reducing execution time using a third-party Helper node, and enhancing efficiency while still preserving data privacy. These optimizations enable MNIST dataset inference in just 32 seconds with only 0.2 GB of RAM for a 5-layer neural network. In contrast, the previous baseline implementation required 8.03 GB of RAM and 200 seconds of execution time.

Active-LATHE: An Active Learning Algorithm for Boosting the Error Exponent for Learning Homogeneous Ising Trees

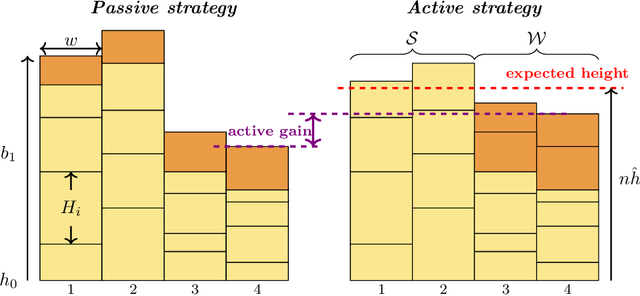
The Chow-Liu algorithm (IEEE Trans.~Inform.~Theory, 1968) has been a mainstay for the learning of tree-structured graphical models from i.i.d.\ sampled data vectors. Its theoretical properties have been well-studied and are well-understood. In this paper, we focus on the class of trees that are arguably even more fundamental, namely {\em homogeneous} trees in which each pair of nodes that forms an edge has the same correlation $\rho$. We ask whether we are able to further reduce the error probability of learning the structure of the homogeneous tree model when {\em active learning} or {\em active sampling of nodes or variables} is allowed. Our figure of merit is the {\em error exponent}, which quantifies the exponential rate of decay of the error probability with an increasing number of data samples. At first sight, an improvement in the error exponent seems impossible, as all the edges are statistically identical. We design and analyze an algorithm Active Learning Algorithm for Trees with Homogeneous Edge (Active-LATHE), which surprisingly boosts the error exponent by at least 40\% when $\rho$ is at least $0.8$. For all other values of $\rho$, we also observe commensurate, but more modest, improvements in the error exponent. Our analysis hinges on judiciously exploiting the minute but detectable statistical variation of the samples to allocate more data to parts of the graph in which we are less confident of being correct.

SGA: A Robust Algorithm for Partial Recovery of Tree-Structured Graphical Models with Noisy Samples

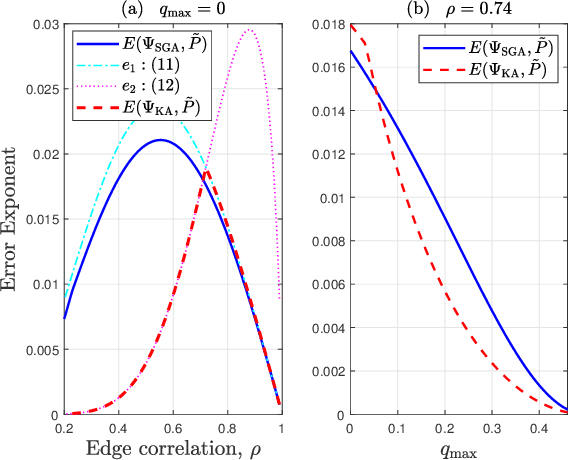
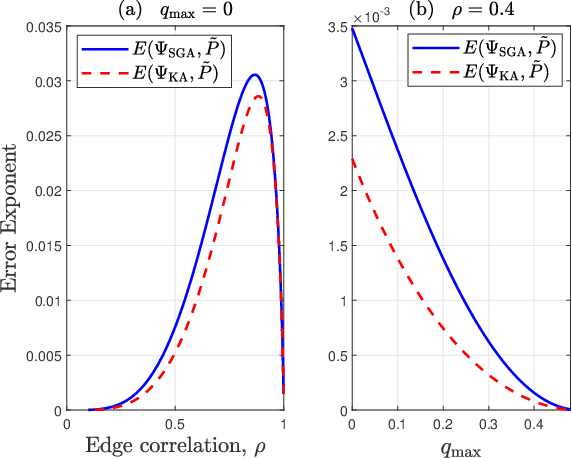
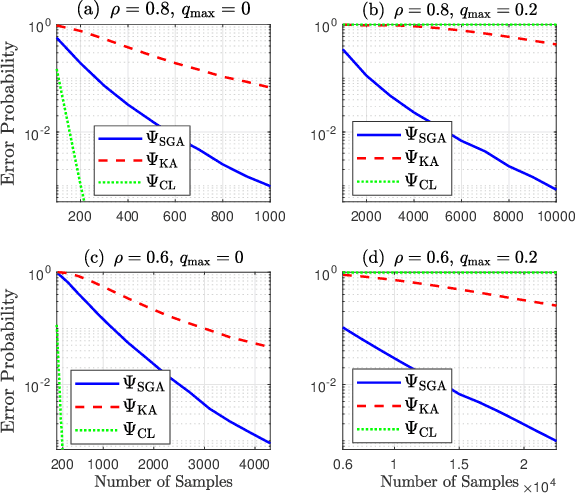
We consider learning Ising tree models when the observations from the nodes are corrupted by independent but non-identically distributed noise with unknown statistics. Katiyar et al. (2020) showed that although the exact tree structure cannot be recovered, one can recover a partial tree structure; that is, a structure belonging to the equivalence class containing the true tree. This paper presents a systematic improvement of Katiyar et al. (2020). First, we present a novel impossibility result by deriving a bound on the necessary number of samples for partial recovery. Second, we derive a significantly improved sample complexity result in which the dependence on the minimum correlation $\rho_{\min}$ is $\rho_{\min}^{-8}$ instead of $\rho_{\min}^{-24}$. Finally, we propose Symmetrized Geometric Averaging (SGA), a more statistically robust algorithm for partial tree recovery. We provide error exponent analyses and extensive numerical results on a variety of trees to show that the sample complexity of SGA is significantly better than the algorithm of Katiyar et al. (2020). SGA can be readily extended to Gaussian models and is shown via numerical experiments to be similarly superior.

Exact Asymptotics for Learning Tree-Structured Graphical Models with Side Information: Noiseless and Noisy Samples

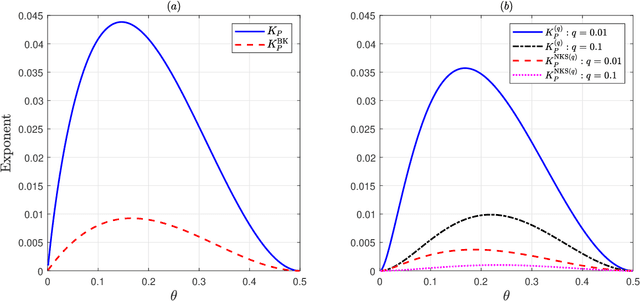
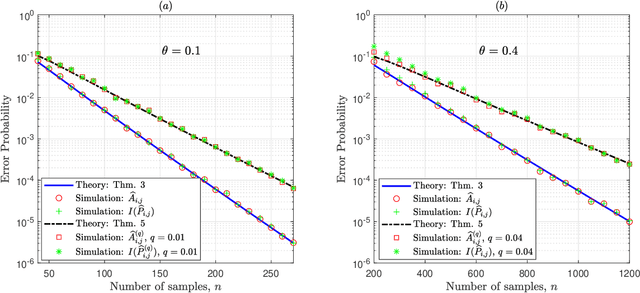
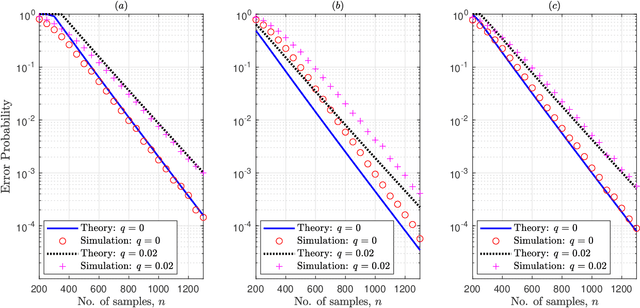
Given side information that an Ising tree-structured graphical model is homogeneous and has no external field, we derive the exact asymptotics of learning its structure from independently drawn samples. Our results, which leverage the use of probabilistic tools from the theory of strong large deviations, refine the large deviation (error exponents) results of Tan, Anandkumar, Tong, and Willsky [IEEE Trans. on Inform. Th., 57(3):1714--1735, 2011] and strictly improve those of Bresler and Karzand [Ann. Statist., 2020]. In addition, we extend our results to the scenario in which the samples are observed in random noise. In this case, we show that they strictly improve on the recent results of Nikolakakis, Kalogerias, and Sarwate [Proc. AISTATS, 1771--1782, 2019]. Our theoretical results demonstrate keen agreement with experimental results for sample sizes as small as that in the hundreds.