SGA: A Robust Algorithm for Partial Recovery of Tree-Structured Graphical Models with Noisy Samples
Paper and Code
Jan 22, 2021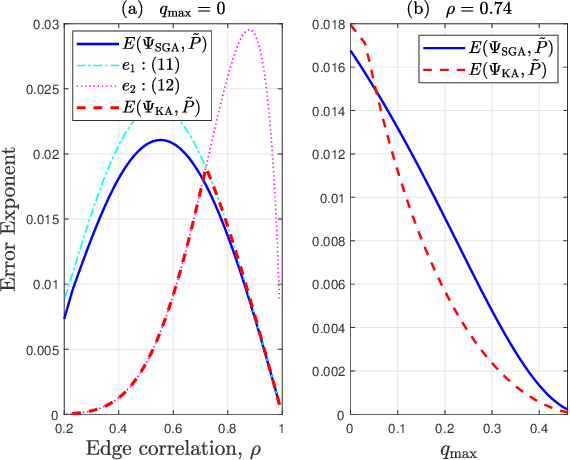
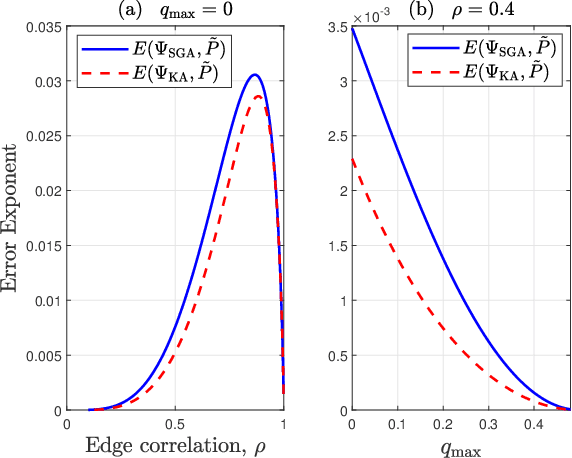
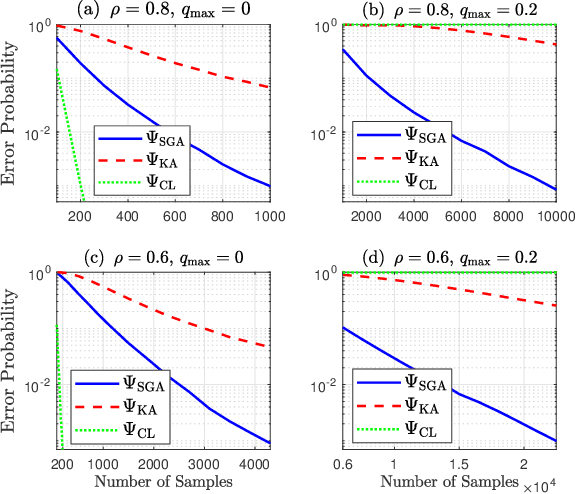

We consider learning Ising tree models when the observations from the nodes are corrupted by independent but non-identically distributed noise with unknown statistics. Katiyar et al. (2020) showed that although the exact tree structure cannot be recovered, one can recover a partial tree structure; that is, a structure belonging to the equivalence class containing the true tree. This paper presents a systematic improvement of Katiyar et al. (2020). First, we present a novel impossibility result by deriving a bound on the necessary number of samples for partial recovery. Second, we derive a significantly improved sample complexity result in which the dependence on the minimum correlation $\rho_{\min}$ is $\rho_{\min}^{-8}$ instead of $\rho_{\min}^{-24}$. Finally, we propose Symmetrized Geometric Averaging (SGA), a more statistically robust algorithm for partial tree recovery. We provide error exponent analyses and extensive numerical results on a variety of trees to show that the sample complexity of SGA is significantly better than the algorithm of Katiyar et al. (2020). SGA can be readily extended to Gaussian models and is shown via numerical experiments to be similarly superior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge