Exact Asymptotics for Learning Tree-Structured Graphical Models with Side Information: Noiseless and Noisy Samples
Paper and Code
May 09, 2020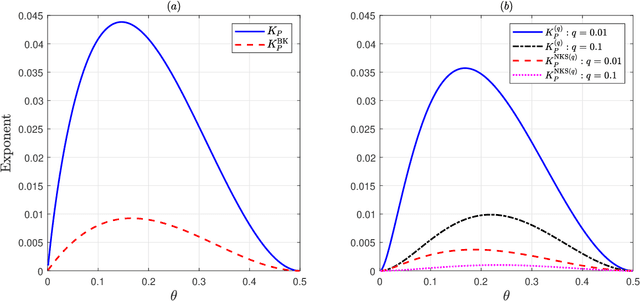
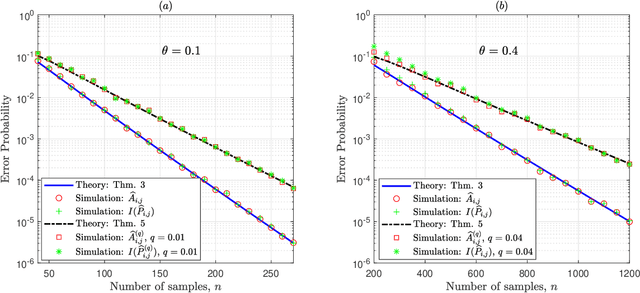
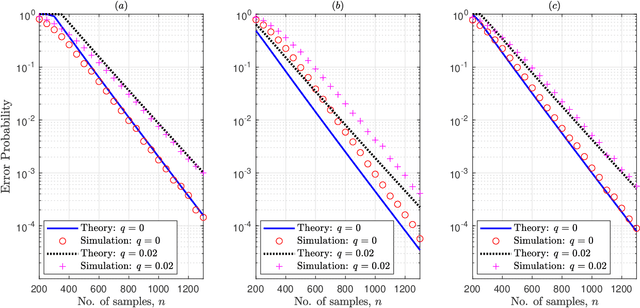
Given side information that an Ising tree-structured graphical model is homogeneous and has no external field, we derive the exact asymptotics of learning its structure from independently drawn samples. Our results, which leverage the use of probabilistic tools from the theory of strong large deviations, refine the large deviation (error exponents) results of Tan, Anandkumar, Tong, and Willsky [IEEE Trans. on Inform. Th., 57(3):1714--1735, 2011] and strictly improve those of Bresler and Karzand [Ann. Statist., 2020]. In addition, we extend our results to the scenario in which the samples are observed in random noise. In this case, we show that they strictly improve on the recent results of Nikolakakis, Kalogerias, and Sarwate [Proc. AISTATS, 1771--1782, 2019]. Our theoretical results demonstrate keen agreement with experimental results for sample sizes as small as that in the hundreds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge