Efficient Flow Matching using Latent Variables

Flow matching models have shown great potential in image generation tasks among probabilistic generative models. Building upon the ideas of continuous normalizing flows, flow matching models generalize the transport path of the diffusion models from a simple prior distribution to the data. Most flow matching models in the literature do not explicitly model the underlying structure/manifold in the target data when learning the flow from a simple source distribution like the standard Gaussian. This leads to inefficient learning, especially for many high-dimensional real-world datasets, which often reside in a low-dimensional manifold. Existing strategies of incorporating manifolds, including data with underlying multi-modal distribution, often require expensive training and hence frequently lead to suboptimal performance. To this end, we present \texttt{Latent-CFM}, which provides simplified training/inference strategies to incorporate multi-modal data structures using pretrained deep latent variable models. Through experiments on multi-modal synthetic data and widely used image benchmark datasets, we show that \texttt{Latent-CFM} exhibits improved generation quality with significantly less training ($\sim 50\%$ less in some cases) and computation than state-of-the-art flow matching models. Using a 2d Darcy flow dataset, we demonstrate that our approach generates more physically accurate samples than competitive approaches. In addition, through latent space analysis, we demonstrate that our approach can be used for conditional image generation conditioned on latent features.

REMEDI: Corrective Transformations for Improved Neural Entropy Estimation

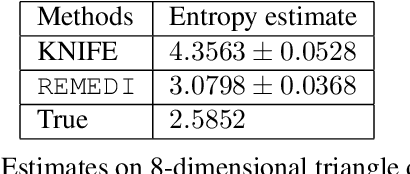
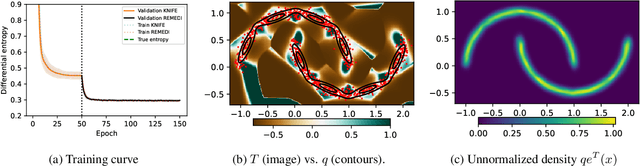
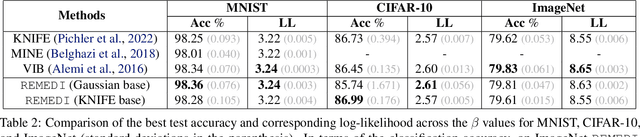
Information theoretic quantities play a central role in machine learning. The recent surge in the complexity of data and models has increased the demand for accurate estimation of these quantities. However, as the dimension grows the estimation presents significant challenges, with existing methods struggling already in relatively low dimensions. To address this issue, in this work, we introduce $\texttt{REMEDI}$ for efficient and accurate estimation of differential entropy, a fundamental information theoretic quantity. The approach combines the minimization of the cross-entropy for simple, adaptive base models and the estimation of their deviation, in terms of the relative entropy, from the data density. Our approach demonstrates improvement across a broad spectrum of estimation tasks, encompassing entropy estimation on both synthetic and natural data. Further, we extend important theoretical consistency results to a more generalized setting required by our approach. We illustrate how the framework can be naturally extended to information theoretic supervised learning models, with a specific focus on the Information Bottleneck approach. It is demonstrated that the method delivers better accuracy compared to the existing methods in Information Bottleneck. In addition, we explore a natural connection between $\texttt{REMEDI}$ and generative modeling using rejection sampling and Langevin dynamics.

Sparsity-Inducing Categorical Prior Improves Robustness of the Information Bottleneck

The information bottleneck framework provides a systematic approach to learn representations that compress nuisance information in inputs and extract semantically meaningful information about the predictions. However, the choice of the prior distribution that fix the dimensionality across all the data can restrict the flexibility of this approach to learn robust representations. We present a novel sparsity-inducing spike-slab prior that uses sparsity as a mechanism to provide flexibility that allows each data point to learn its own dimension distribution. In addition, it provides a mechanism to learn a joint distribution of the latent variable and the sparsity. Thus, unlike other approaches, it can account for the full uncertainty in the latent space. Through a series of experiments using in-distribution and out-of-distribution learning scenarios on the MNIST and Fashion-MNIST data we show that the proposed approach improves the accuracy and robustness compared with the traditional fixed -imensional priors as well as other sparsity-induction mechanisms proposed in the literature.