Data-driven decision-making under uncertainty with entropic risk measure

The entropic risk measure is widely used in high-stakes decision making to account for tail risks associated with an uncertain loss. With limited data, the empirical entropic risk estimator, i.e. replacing the expectation in the entropic risk measure with a sample average, underestimates the true risk. To debias the empirical entropic risk estimator, we propose a strongly asymptotically consistent bootstrapping procedure. The first step of the procedure involves fitting a distribution to the data, whereas the second step estimates the bias of the empirical entropic risk estimator using bootstrapping, and corrects for it. We show that naively fitting a Gaussian Mixture Model to the data using the maximum likelihood criterion typically leads to an underestimation of the risk. To mitigate this issue, we consider two alternative methods: a more computationally demanding one that fits the distribution of empirical entropic risk, and a simpler one that fits the extreme value distribution. As an application of the approach, we study a distributionally robust entropic risk minimization problem with type-$\infty$ Wasserstein ambiguity set, where debiasing the validation performance using our techniques significantly improves the calibration of the size of the ambiguity set. Furthermore, we propose a distributionally robust optimization model for a well-studied insurance contract design problem. The model considers multiple (potential) policyholders that have dependent risks and the insurer and policyholders use entropic risk measure. We show that cross validation methods can result in significantly higher out-of-sample risk for the insurer if the bias in validation performance is not corrected for. This improvement can be explained from the observation that our methods suggest a higher (and more accurate) premium to homeowners.

Robust Data-driven Prescriptiveness Optimization

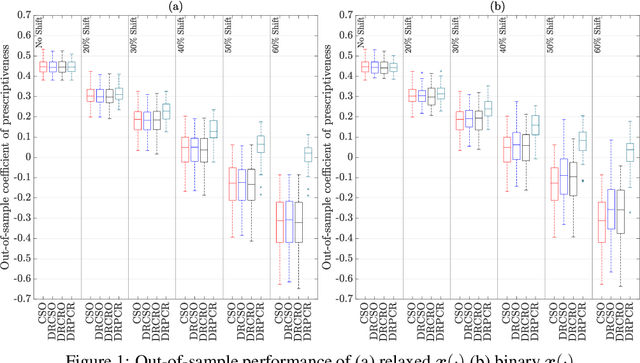
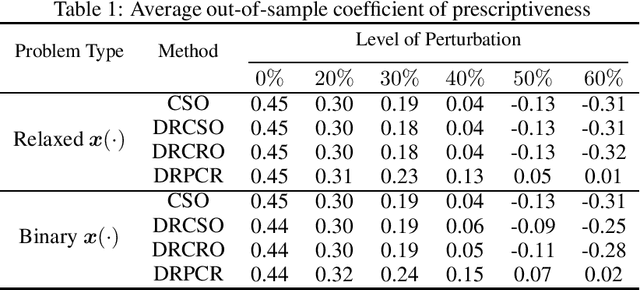
The abundance of data has led to the emergence of a variety of optimization techniques that attempt to leverage available side information to provide more anticipative decisions. The wide range of methods and contexts of application have motivated the design of a universal unitless measure of performance known as the coefficient of prescriptiveness. This coefficient was designed to quantify both the quality of contextual decisions compared to a reference one and the prescriptive power of side information. To identify policies that maximize the former in a data-driven context, this paper introduces a distributionally robust contextual optimization model where the coefficient of prescriptiveness substitutes for the classical empirical risk minimization objective. We present a bisection algorithm to solve this model, which relies on solving a series of linear programs when the distributional ambiguity set has an appropriate nested form and polyhedral structure. Studying a contextual shortest path problem, we evaluate the robustness of the resulting policies against alternative methods when the out-of-sample dataset is subject to varying amounts of distribution shift.

Distributionally Robust Parametric Maximum Likelihood Estimation

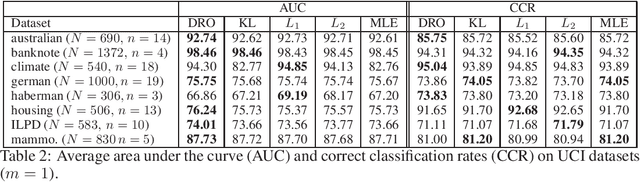
We consider the parameter estimation problem of a probabilistic generative model prescribed using a natural exponential family of distributions. For this problem, the typical maximum likelihood estimator usually overfits under limited training sample size, is sensitive to noise and may perform poorly on downstream predictive tasks. To mitigate these issues, we propose a distributionally robust maximum likelihood estimator that minimizes the worst-case expected log-loss uniformly over a parametric Kullback-Leibler ball around a parametric nominal distribution. Leveraging the analytical expression of the Kullback-Leibler divergence between two distributions in the same natural exponential family, we show that the min-max estimation problem is tractable in a broad setting, including the robust training of generalized linear models. Our novel robust estimator also enjoys statistical consistency and delivers promising empirical results in both regression and classification tasks.