Cleora: A Simple, Strong and Scalable Graph Embedding Scheme

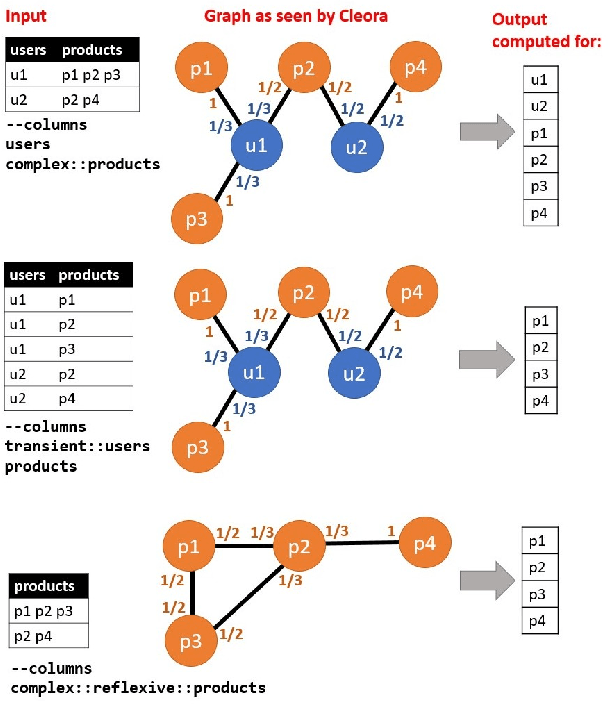
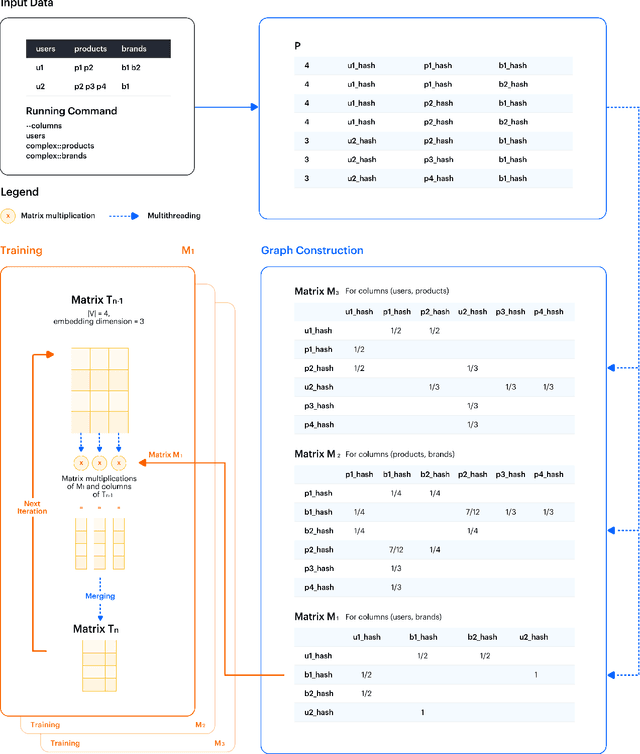
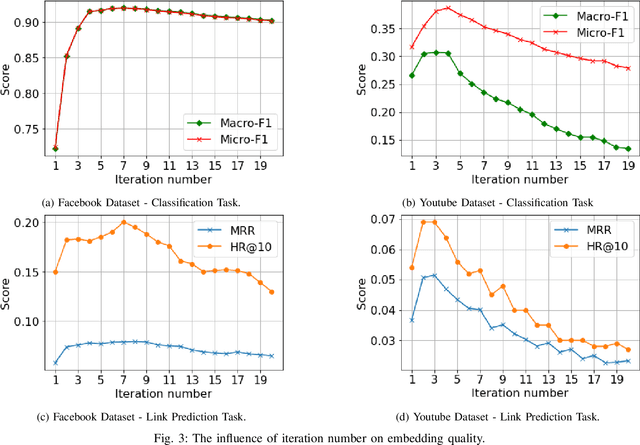
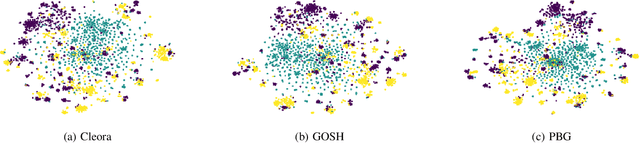
The area of graph embeddings is currently dominated by contrastive learning methods, which demand formulation of an explicit objective function and sampling of positive and negative examples. This creates a conceptual and computational overhead. Simple, classic unsupervised approaches like Multidimensional Scaling (MSD) or the Laplacian eigenmap skip the necessity of tedious objective optimization, directly exploiting data geometry. Unfortunately, their reliance on very costly operations such as matrix eigendecomposition make them unable to scale to large graphs that are common in today's digital world. In this paper we present Cleora: an algorithm which gets the best of two worlds, being both unsupervised and highly scalable. We show that high quality embeddings can be produced without the popular step-wise learning framework with example sampling. An intuitive learning objective of our algorithm is that a node should be similar to its neighbors, without explicitly pushing disconnected nodes apart. The objective is achieved by iterative weighted averaging of node neigbors' embeddings, followed by normalization across dimensions. Thanks to the averaging operation the algorithm makes rapid strides across the embedding space and usually reaches optimal embeddings in just a few iterations. Cleora runs faster than other state-of-the-art CPU algorithms and produces embeddings of competitive quality as measured on downstream tasks: link prediction and node classification. We show that Cleora learns a data abstraction that is similar to contrastive methods, yet at much lower computational cost. We open-source Cleora under the MIT license allowing commercial use under https://github.com/Synerise/cleora.

An efficient manifold density estimator for all recommendation systems

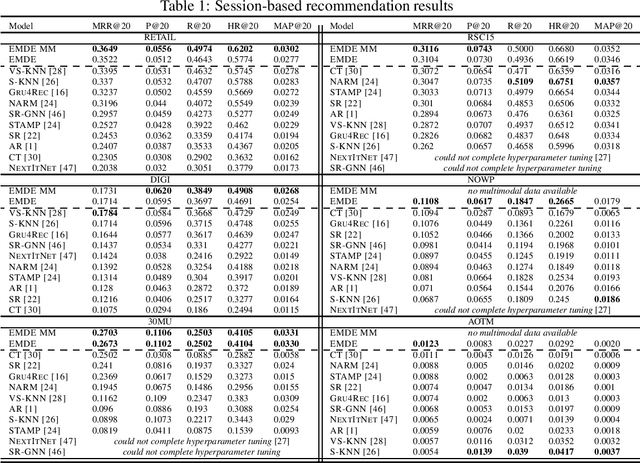
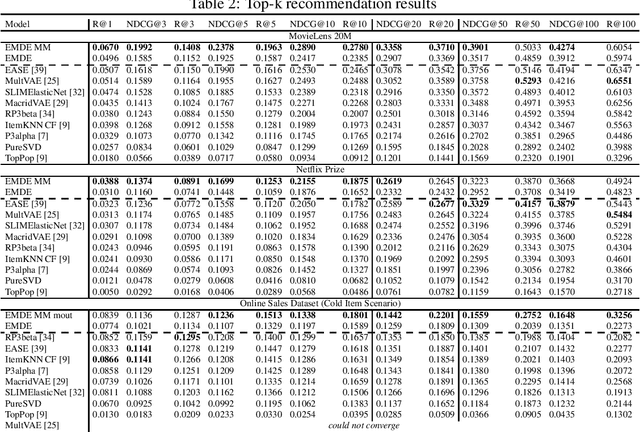
Many unsupervised representation learning methods belong to the class of similarity learning models. While various modality-specific approaches exist for different types of data, a core property of many methods is that representations of similar inputs are close under some similarity function. We propose EMDE (Efficient Manifold Density Estimator) - a framework utilizing arbitrary vector representations with the property of local similarity to succinctly represent smooth probability densities on Riemannian manifolds. Our approximate representation has the desirable properties of being fixed-size and having simple additive compositionality, thus being especially amenable to treatment with neural networks - both as input and output format, producing efficient conditional estimators. We generalize and reformulate the problem of multi-modal recommendations as conditional, weighted density estimation on manifolds. Our approach allows for trivial inclusion of multiple interaction types, modalities of data as well as interaction strengths for any recommendation setting. Applying EMDE to both top-k and session-based recommendation settings, we establish new state-of-the-art results on multiple open datasets in both uni-modal and multi-modal settings. We release the source code and our own real-world dataset of e-commerce product purchases, with special focus on modeling of the item cold-start problem.