Piotr Bąbel
Cleora: A Simple, Strong and Scalable Graph Embedding Scheme
Feb 03, 2021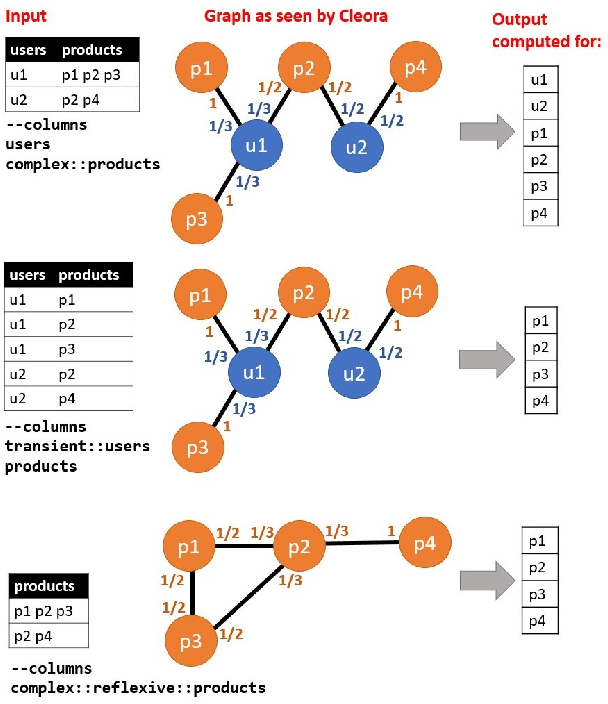
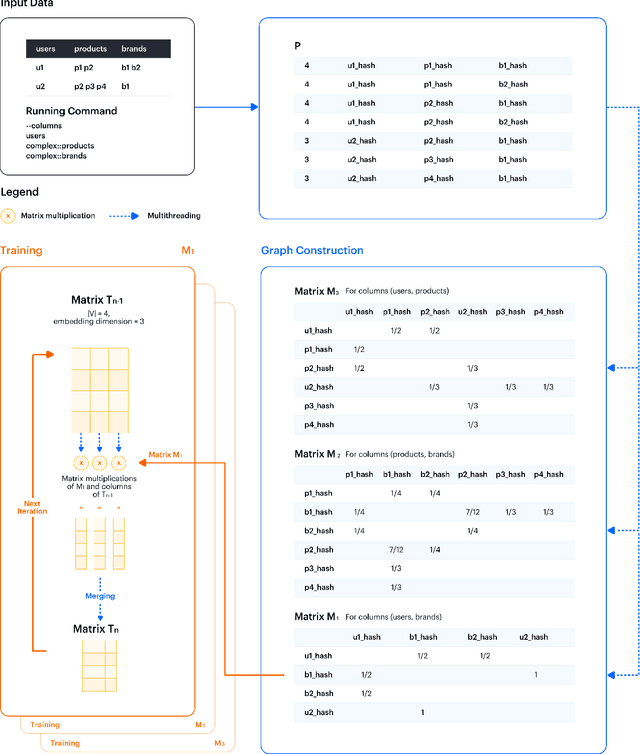
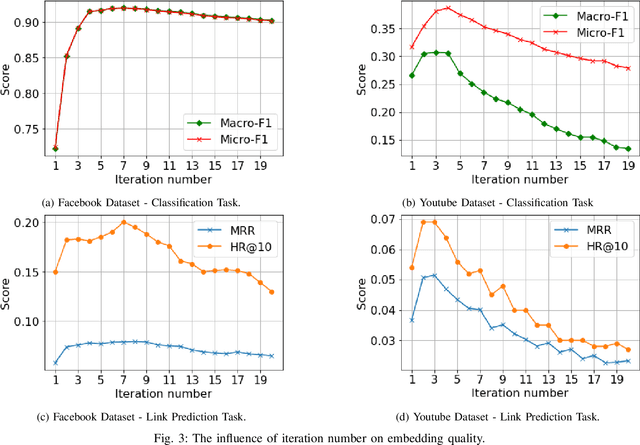
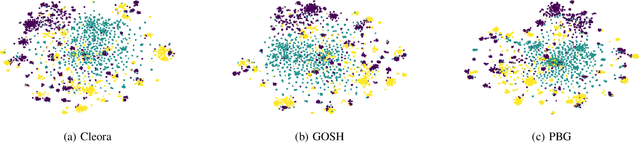
Abstract:The area of graph embeddings is currently dominated by contrastive learning methods, which demand formulation of an explicit objective function and sampling of positive and negative examples. This creates a conceptual and computational overhead. Simple, classic unsupervised approaches like Multidimensional Scaling (MSD) or the Laplacian eigenmap skip the necessity of tedious objective optimization, directly exploiting data geometry. Unfortunately, their reliance on very costly operations such as matrix eigendecomposition make them unable to scale to large graphs that are common in today's digital world. In this paper we present Cleora: an algorithm which gets the best of two worlds, being both unsupervised and highly scalable. We show that high quality embeddings can be produced without the popular step-wise learning framework with example sampling. An intuitive learning objective of our algorithm is that a node should be similar to its neighbors, without explicitly pushing disconnected nodes apart. The objective is achieved by iterative weighted averaging of node neigbors' embeddings, followed by normalization across dimensions. Thanks to the averaging operation the algorithm makes rapid strides across the embedding space and usually reaches optimal embeddings in just a few iterations. Cleora runs faster than other state-of-the-art CPU algorithms and produces embeddings of competitive quality as measured on downstream tasks: link prediction and node classification. We show that Cleora learns a data abstraction that is similar to contrastive methods, yet at much lower computational cost. We open-source Cleora under the MIT license allowing commercial use under https://github.com/Synerise/cleora.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge