Andrew Buck
Fuzzy Integral = Contextual Linear Order Statistic
Jul 06, 2020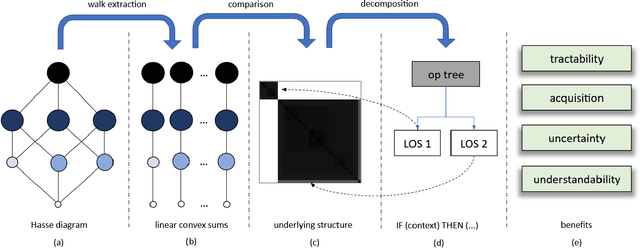
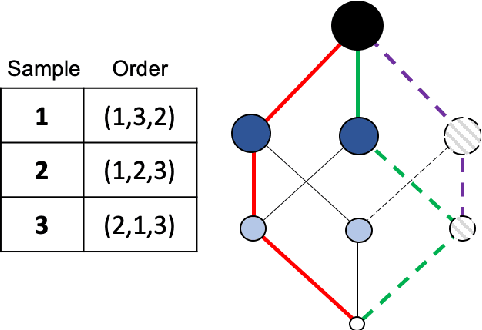
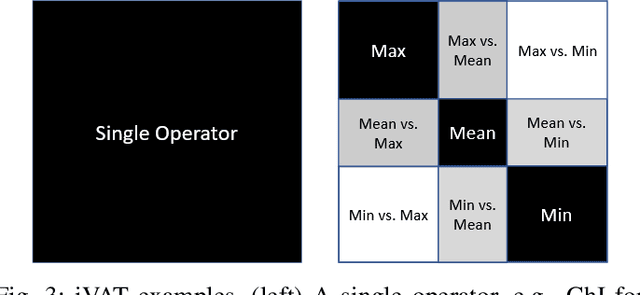

Abstract:The fuzzy integral is a powerful parametric nonlin-ear function with utility in a wide range of applications, from information fusion to classification, regression, decision making,interpolation, metrics, morphology, and beyond. While the fuzzy integral is in general a nonlinear operator, herein we show that it can be represented by a set of contextual linear order statistics(LOS). These operators can be obtained via sampling the fuzzy measure and clustering is used to produce a partitioning of the underlying space of linear convex sums. Benefits of our approach include scalability, improved integral/measure acquisition, generalizability, and explainable/interpretable models. Our methods are both demonstrated on controlled synthetic experiments, and also analyzed and validated with real-world benchmark data sets.
Deep Morphological Hit-or-Miss Transform Neural Network
Dec 04, 2019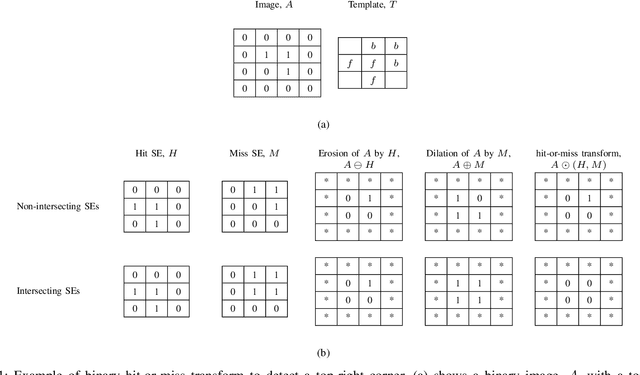



Abstract:Neural networks have demonstrated breakthrough results in numerous application domains. While most architectures are built on the premise of convolution, alternative foundations like morphology are being explored for reasons like interpretability and its connection to the analysis and processing of geometric structures. Herein, we investigate new deep networks based on the morphological hit-or-miss transform. The hit-or-miss takes into account both foreground and background when measuring the fitness of a target shape in an image. We identify limitations of current hit-or-miss definitions, and we formulate an optimization problem to learn the transform. Our analysis shows that convolution, in fact, acts like a hit-miss transform through semantic interpretation of its filter differences. Analogous to the generalized hit-or-miss transform, we also introduce an extension of convolution and show that it outperforms conventional convolution on benchmark data sets. We conducted experiments on synthetic and benchmark data sets, and we show that the direct encoding hit-or-miss transform provides better interpretability on learned shapes consistent with objects whereas our morphologically inspired generalized convolution yields higher classification accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge