Matthew Deardorff
Fuzzy Integral = Contextual Linear Order Statistic
Jul 06, 2020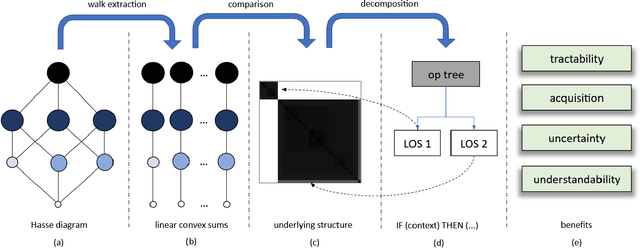
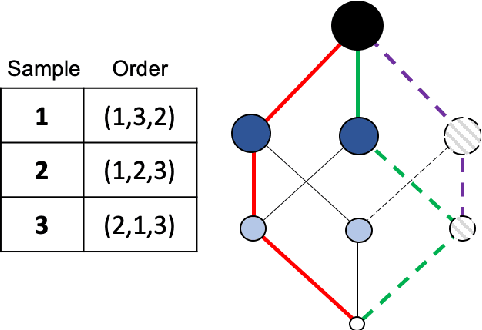
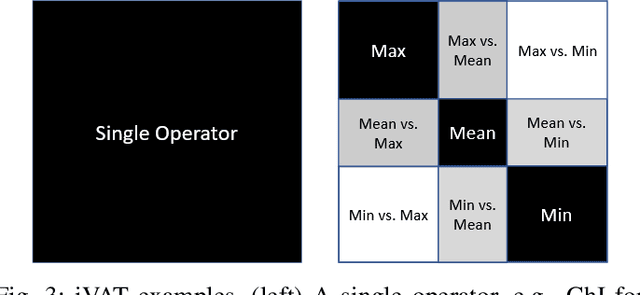

Abstract:The fuzzy integral is a powerful parametric nonlin-ear function with utility in a wide range of applications, from information fusion to classification, regression, decision making,interpolation, metrics, morphology, and beyond. While the fuzzy integral is in general a nonlinear operator, herein we show that it can be represented by a set of contextual linear order statistics(LOS). These operators can be obtained via sampling the fuzzy measure and clustering is used to produce a partitioning of the underlying space of linear convex sums. Benefits of our approach include scalability, improved integral/measure acquisition, generalizability, and explainable/interpretable models. Our methods are both demonstrated on controlled synthetic experiments, and also analyzed and validated with real-world benchmark data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge