Fuzzy Integral = Contextual Linear Order Statistic

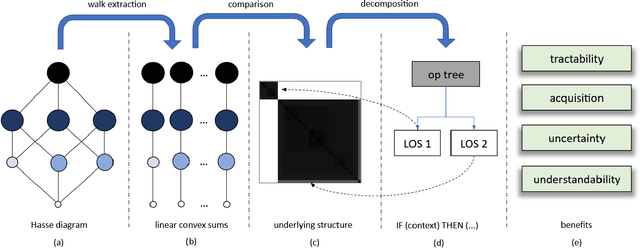
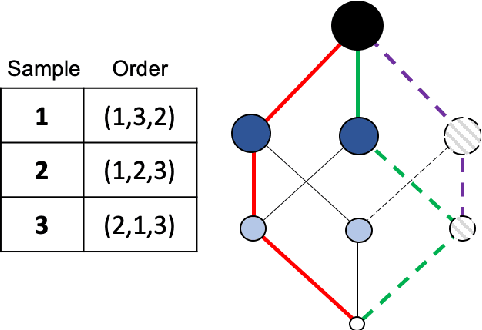
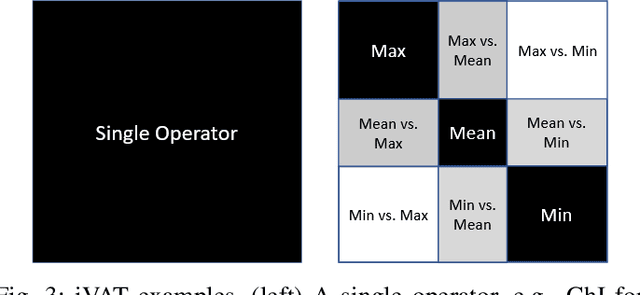
The fuzzy integral is a powerful parametric nonlin-ear function with utility in a wide range of applications, from information fusion to classification, regression, decision making,interpolation, metrics, morphology, and beyond. While the fuzzy integral is in general a nonlinear operator, herein we show that it can be represented by a set of contextual linear order statistics(LOS). These operators can be obtained via sampling the fuzzy measure and clustering is used to produce a partitioning of the underlying space of linear convex sums. Benefits of our approach include scalability, improved integral/measure acquisition, generalizability, and explainable/interpretable models. Our methods are both demonstrated on controlled synthetic experiments, and also analyzed and validated with real-world benchmark data sets.

Convolutional Neural Networks for Aircraft Noise Monitoring

Air travel is one of the fastest growing modes of transportation, however, the effects of aircraft noise on populations surrounding airports is hindering its growth. In an effort to study and ultimately mitigate the impact that this noise has, many airports continuously monitor the aircraft noise in their surrounding communities. Noise monitoring and analysis is complicated by the fact that aircraft are not the only source of noise. In this work, we show that a Convolutional Neural Network is well-suited for the task of identifying noise events which are not caused by aircraft. Our system achieves an accuracy of 0.970 when trained on 900 manually labeled noise events. Our training data and a TensorFlow implementation of our model are available at https://github.com/neheller/aircraftnoise.