Employing an Adjusted Stability Measure for Multi-Criteria Model Fitting on Data Sets with Similar Features

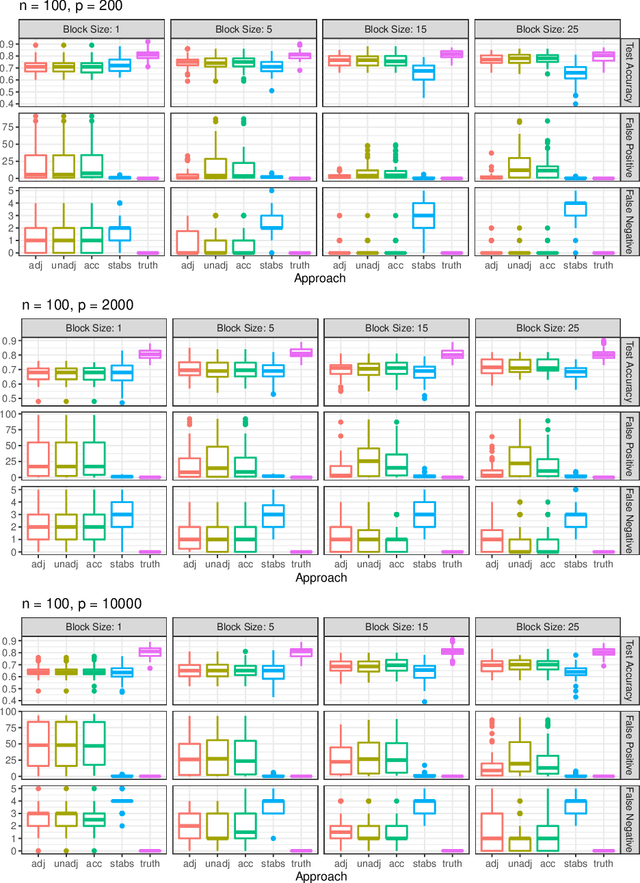
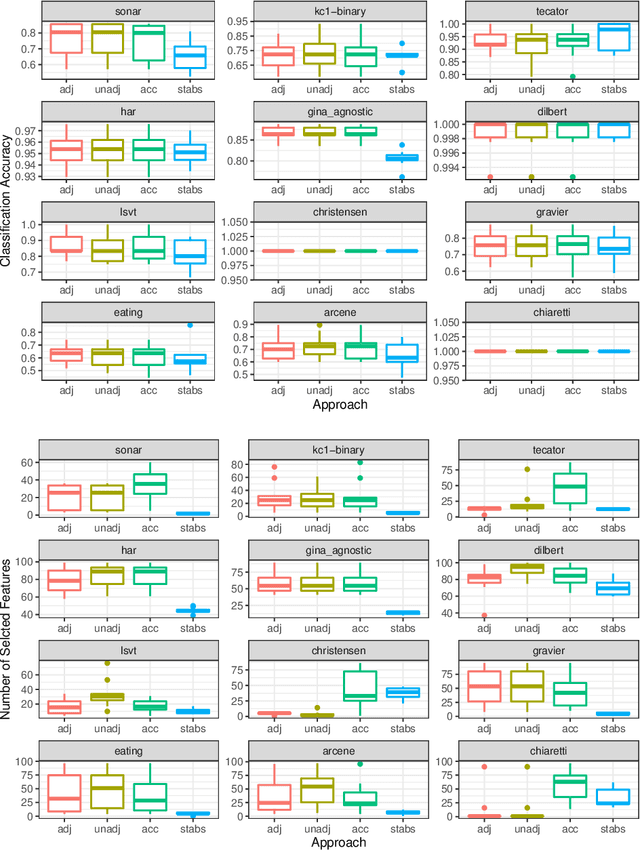
Fitting models with high predictive accuracy that include all relevant but no irrelevant or redundant features is a challenging task on data sets with similar (e.g. highly correlated) features. We propose the approach of tuning the hyperparameters of a predictive model in a multi-criteria fashion with respect to predictive accuracy and feature selection stability. We evaluate this approach based on both simulated and real data sets and we compare it to the standard approach of single-criteria tuning of the hyperparameters as well as to the state-of-the-art technique "stability selection". We conclude that our approach achieves the same or better predictive performance compared to the two established approaches. Considering the stability during tuning does not decrease the predictive accuracy of the resulting models. Our approach succeeds at selecting the relevant features while avoiding irrelevant or redundant features. The single-criteria approach fails at avoiding irrelevant or redundant features and the stability selection approach fails at selecting enough relevant features for achieving acceptable predictive accuracy. For our approach, for data sets with many similar features, the feature selection stability must be evaluated with an adjusted stability measure, that is, a measure that considers similarities between features. For data sets with only few similar features, an unadjusted stability measure suffices and is faster to compute.

Adjusted Measures for Feature Selection Stability for Data Sets with Similar Features

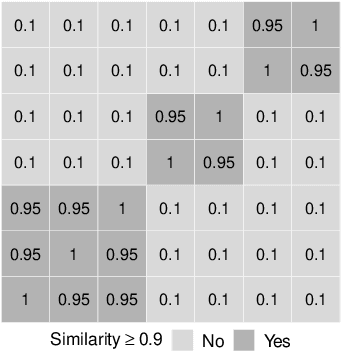
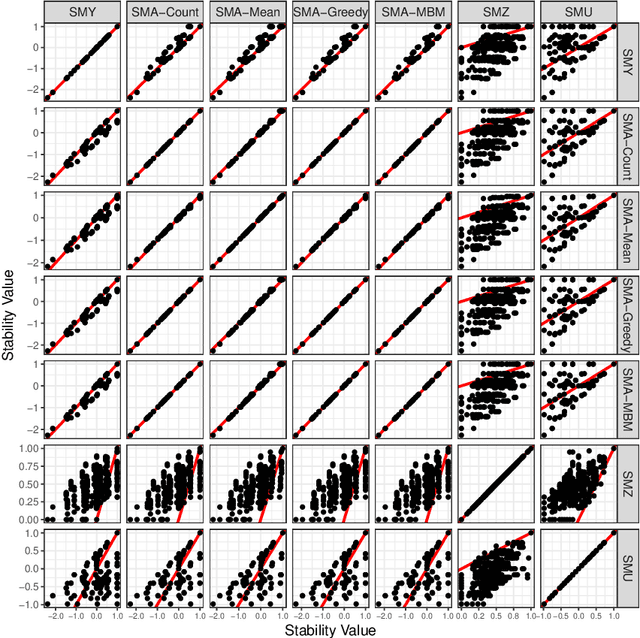
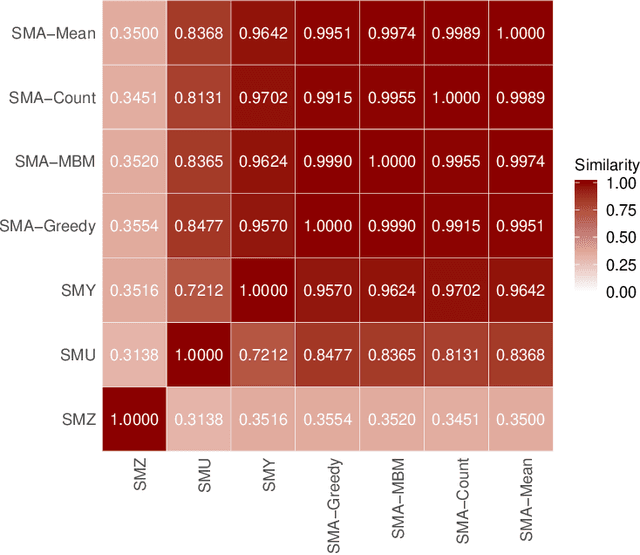
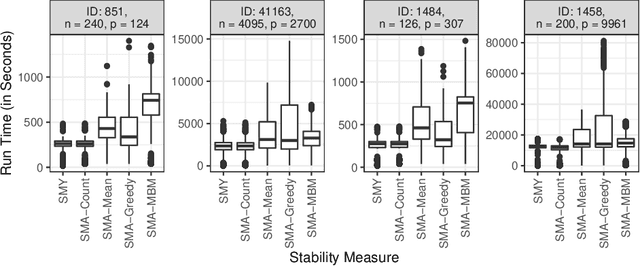
For data sets with similar features, for example highly correlated features, most existing stability measures behave in an undesired way: They consider features that are almost identical but have different identifiers as different features. Existing adjusted stability measures, that is, stability measures that take into account the similarities between features, have major theoretical drawbacks. We introduce new adjusted stability measures that overcome these drawbacks. We compare them to each other and to existing stability measures based on both artificial and real sets of selected features. Based on the results, we suggest using one new stability measure that considers highly similar features as exchangeable.

High Dimensional Restrictive Federated Model Selection with multi-objective Bayesian Optimization over shifted distributions

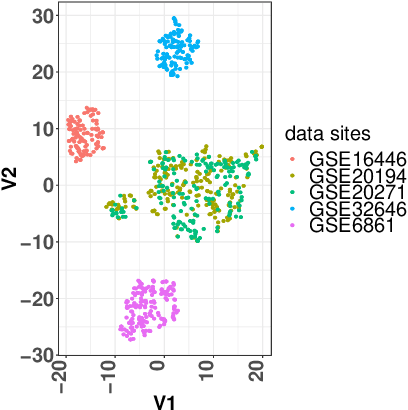
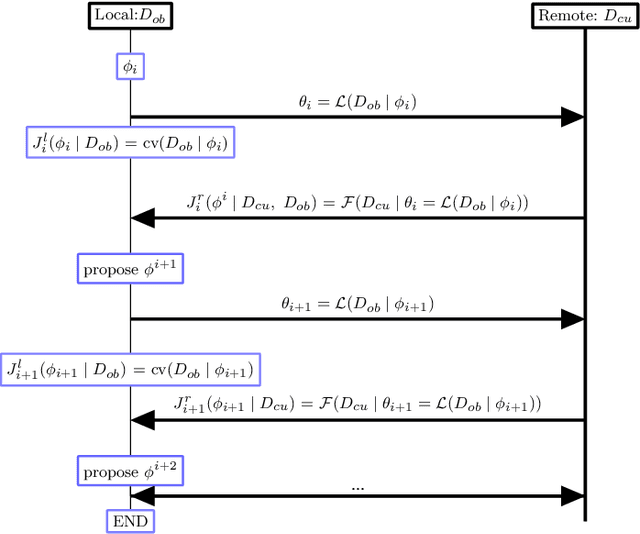
A novel machine learning optimization process coined Restrictive Federated Model Selection (RFMS) is proposed under the scenario, for example, when data from healthcare units can not leave the site it is situated on and it is forbidden to carry out training algorithms on remote data sites due to either technical or privacy and trust concerns. To carry out a clinical research under this scenario, an analyst could train a machine learning model only on local data site, but it is still possible to execute a statistical query at a certain cost in the form of sending a machine learning model to some of the remote data sites and get the performance measures as feedback, maybe due to prediction being usually much cheaper. Compared to federated learning, which is optimizing the model parameters directly by carrying out training across all data sites, RFMS trains model parameters only on one local data site but optimizes hyper-parameters across other data sites jointly since hyper-parameters play an important role in machine learning performance. The aim is to get a Pareto optimal model with respective to both local and remote unseen prediction losses, which could generalize well across data sites. In this work, we specifically consider high dimensional data with shifted distributions over data sites. As an initial investigation, Bayesian Optimization especially multi-objective Bayesian Optimization is used to guide an adaptive hyper-parameter optimization process to select models under the RFMS scenario. Empirical results show that solely using the local data site to tune hyper-parameters generalizes poorly across data sites, compared to methods that utilize the local and remote performances. Furthermore, in terms of dominated hypervolumes, multi-objective Bayesian Optimization algorithms show increased performance across multiple data sites among other candidates.