MARCO: A Memory-Augmented Reinforcement Framework for Combinatorial Optimization

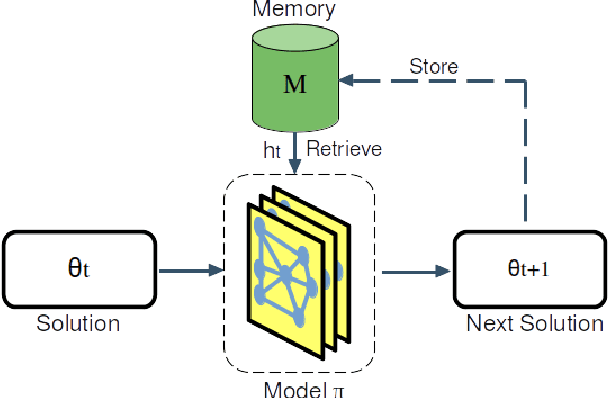
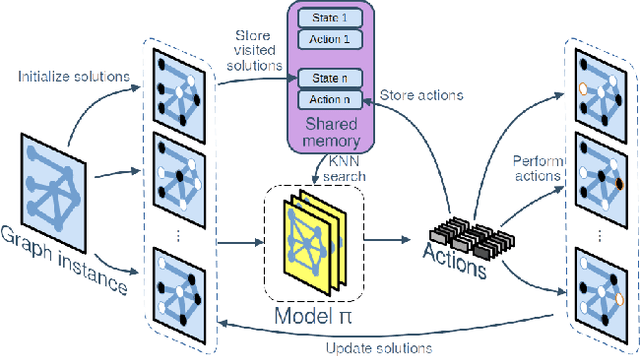
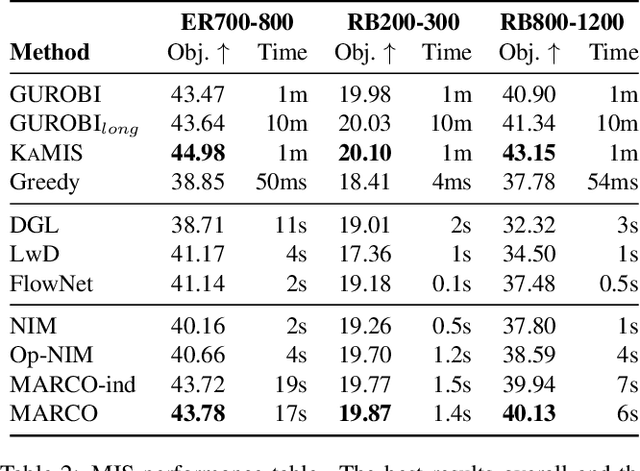
Neural Combinatorial Optimization (NCO) is an emerging domain where deep learning techniques are employed to address combinatorial optimization problems as a standalone solver. Despite their potential, existing NCO methods often suffer from inefficient search space exploration, frequently leading to local optima entrapment or redundant exploration of previously visited states. This paper introduces a versatile framework, referred to as Memory-Augmented Reinforcement for Combinatorial Optimization (MARCO), that can be used to enhance both constructive and improvement methods in NCO through an innovative memory module. MARCO stores data collected throughout the optimization trajectory and retrieves contextually relevant information at each state. This way, the search is guided by two competing criteria: making the best decision in terms of the quality of the solution and avoiding revisiting already explored solutions. This approach promotes a more efficient use of the available optimization budget. Moreover, thanks to the parallel nature of NCO models, several search threads can run simultaneously, all sharing the same memory module, enabling an efficient collaborative exploration. Empirical evaluations, carried out on the maximum cut, maximum independent set and travelling salesman problems, reveal that the memory module effectively increases the exploration, enabling the model to discover diverse, higher-quality solutions. MARCO achieves good performance in a low computational cost, establishing a promising new direction in the field of NCO.

Neural Improvement Heuristics for Preference Ranking

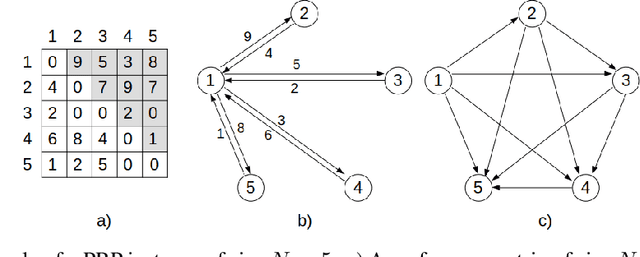
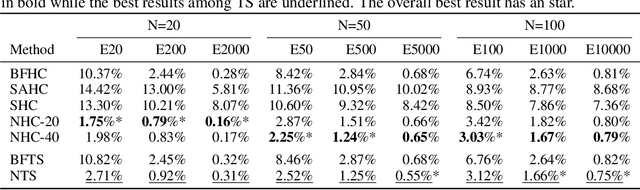
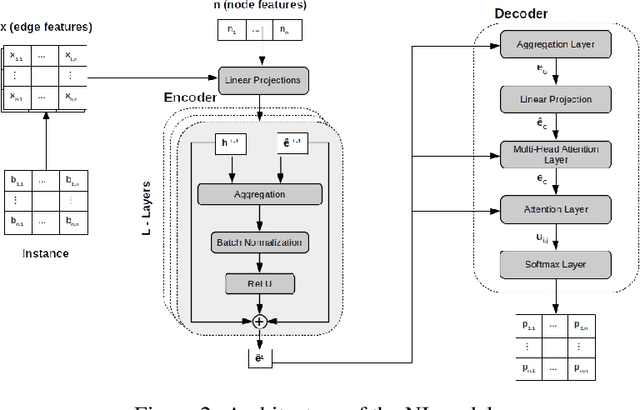
In recent years, Deep Learning based methods have been a revolution in the field of combinatorial optimization. They learn to approximate solutions and constitute an interesting choice when dealing with repetitive problems drawn from similar distributions. Most effort has been devoted to investigating neural constructive methods, while the works that propose neural models to iteratively improve a candidate solution are less frequent. In this paper, we present a Neural Improvement (NI) model for graph-based combinatorial problems that, given an instance and a candidate solution, encodes the problem information by means of edge features. Our model proposes a modification on the pairwise precedence of items to increase the quality of the solution. We demonstrate the practicality of the model by applying it as the building block of a Neural Hill Climber and other trajectory-based methods. The algorithms are used to solve the Preference Ranking Problem and results show that they outperform conventional alternatives in simulated and real-world data. Conducted experiments also reveal that the proposed model can be a milestone in the development of efficiently guided trajectory-based optimization algorithms.

Neural Combinatorial Optimization: a New Player in the Field

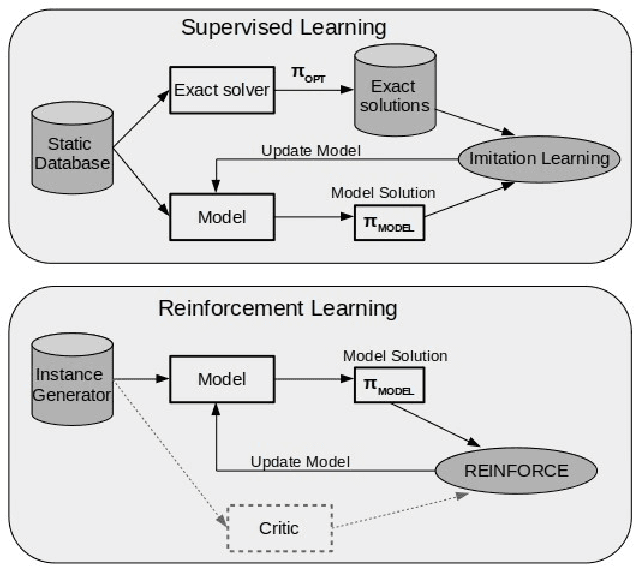
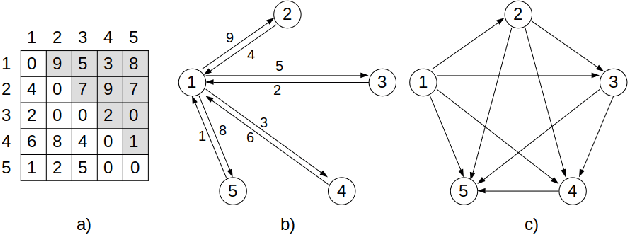
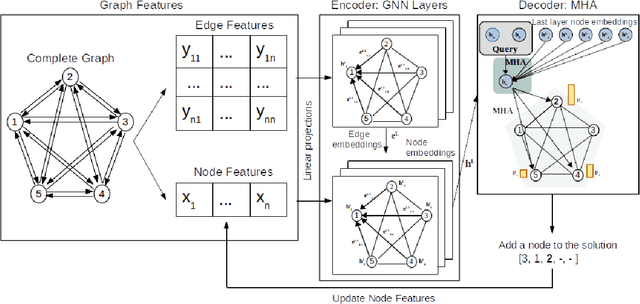
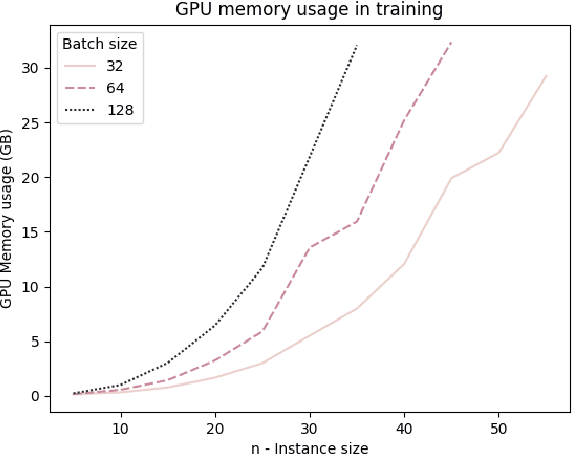
Neural Combinatorial Optimization attempts to learn good heuristics for solving a set of problems using Neural Network models and Reinforcement Learning. Recently, its good performance has encouraged many practitioners to develop neural architectures for a wide variety of combinatorial problems. However, the incorporation of such algorithms in the conventional optimization framework has raised many questions related to their performance and the experimental comparison with other methods such as exact algorithms, heuristics and metaheuristics. This paper presents a critical analysis on the incorporation of algorithms based on neural networks into the classical combinatorial optimization framework. Subsequently, a comprehensive study is carried out to analyse the fundamental aspects of such algorithms, including performance, transferability, computational cost and generalization to larger-sized instances. To that end, we select the Linear Ordering Problem as a case of study, an NP-hard problem, and develop a Neural Combinatorial Optimization model to optimize it. Finally, we discuss how the analysed aspects apply to a general learning framework, and suggest new directions for future work in the area of Neural Combinatorial Optimization algorithms.