Neural Combinatorial Optimization: a New Player in the Field
Paper and Code
May 03, 2022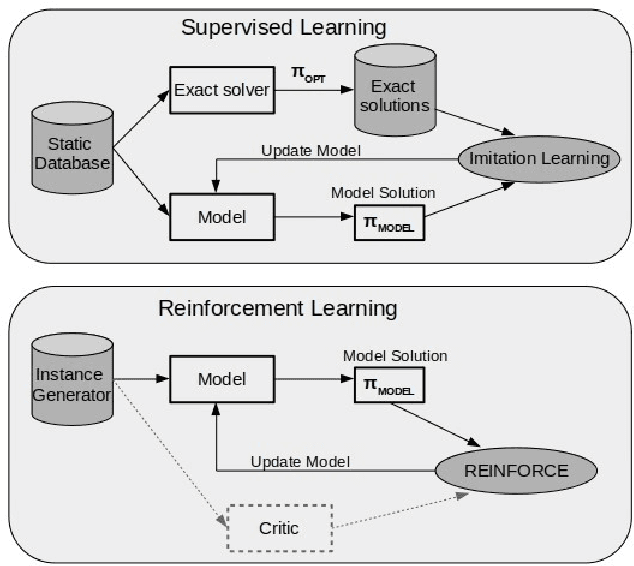
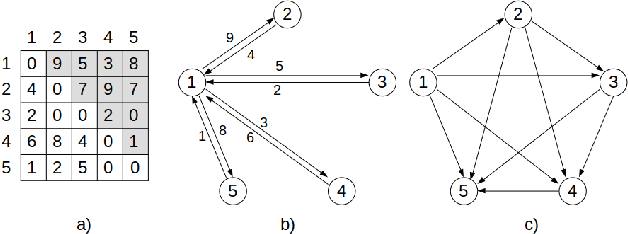
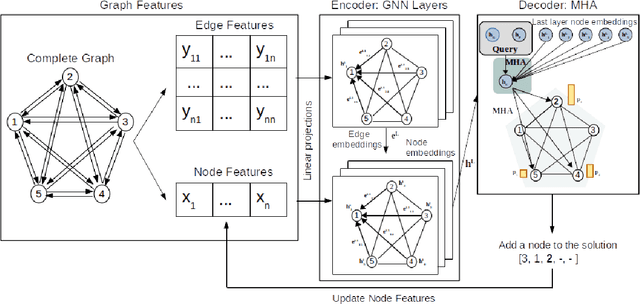
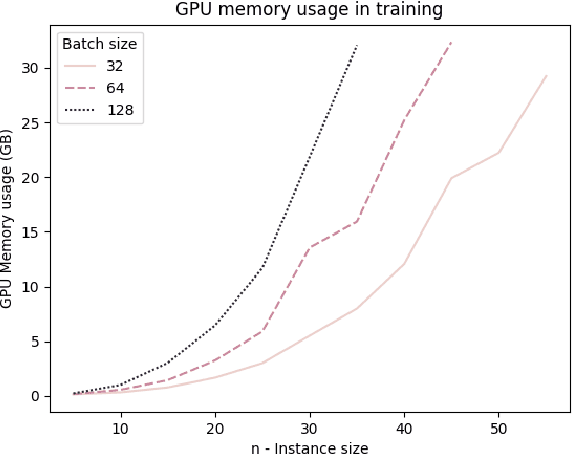
Neural Combinatorial Optimization attempts to learn good heuristics for solving a set of problems using Neural Network models and Reinforcement Learning. Recently, its good performance has encouraged many practitioners to develop neural architectures for a wide variety of combinatorial problems. However, the incorporation of such algorithms in the conventional optimization framework has raised many questions related to their performance and the experimental comparison with other methods such as exact algorithms, heuristics and metaheuristics. This paper presents a critical analysis on the incorporation of algorithms based on neural networks into the classical combinatorial optimization framework. Subsequently, a comprehensive study is carried out to analyse the fundamental aspects of such algorithms, including performance, transferability, computational cost and generalization to larger-sized instances. To that end, we select the Linear Ordering Problem as a case of study, an NP-hard problem, and develop a Neural Combinatorial Optimization model to optimize it. Finally, we discuss how the analysed aspects apply to a general learning framework, and suggest new directions for future work in the area of Neural Combinatorial Optimization algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge