Extracting the Subhalo Mass Function from Strong Lens Images with Image Segmentation

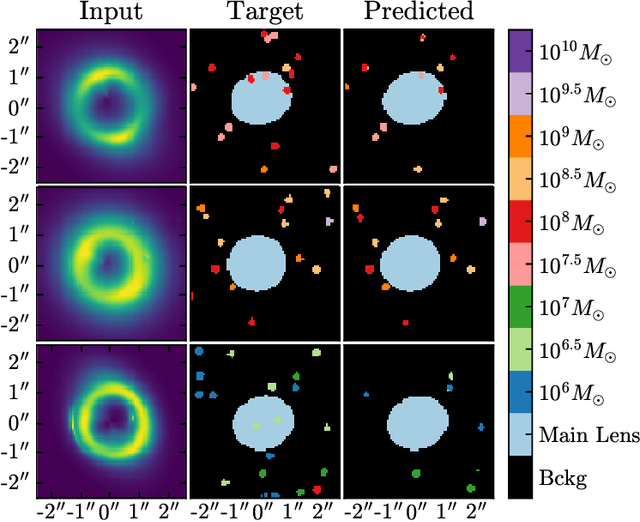
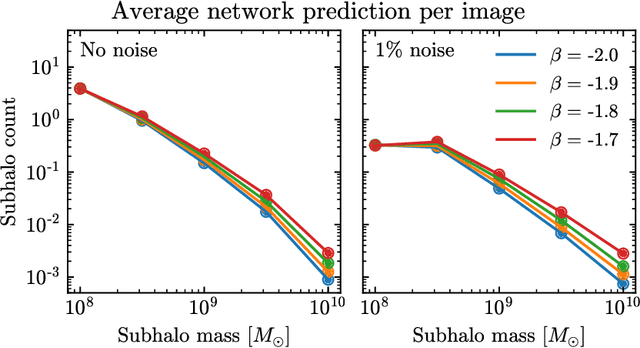
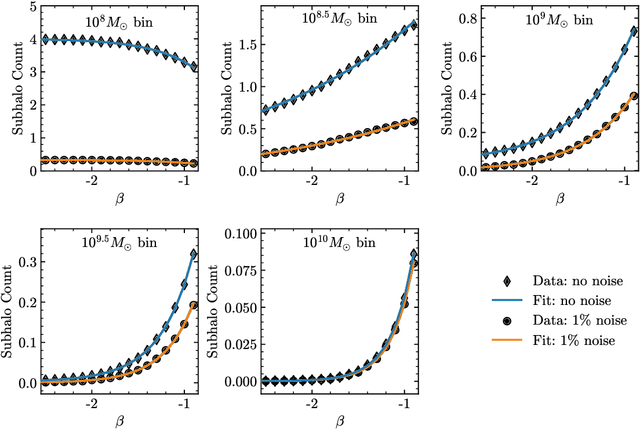
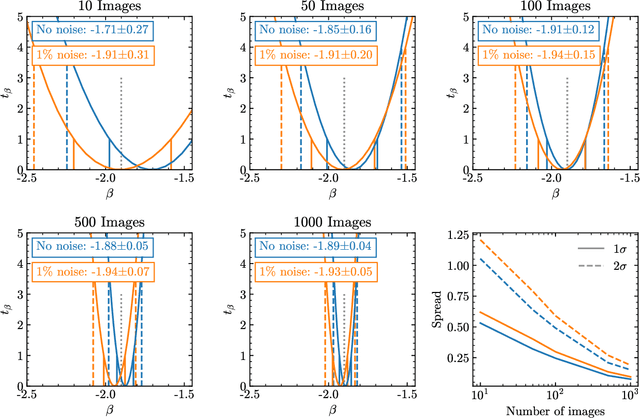
Detecting substructure within strongly lensed images is a promising route to shed light on the nature of dark matter. It is a challenging task, which traditionally requires detailed lens modeling and source reconstruction, taking weeks to analyze each system. We use machine learning to circumvent the need for lens and source modeling and develop a method to both locate subhalos in an image as well as determine their mass using the technique of image segmentation. The network is trained on images with a single subhalo located near the Einstein ring. Training in this way allows the network to learn the gravitational lensing of light and it is then able to accurately detect entire populations of substructure, even far from the Einstein ring. In images with a single subhalo and without noise, the network detects subhalos of mass $10^6 M_{\odot}$ 62% of the time and 78% of these detected subhalos are predicted in the correct mass bin. The detection accuracy increases for heavier masses. When random noise at the level of 1% of the mean brightness of the image is included (which is a realistic approximation HST, for sources brighter than magnitude 20), the network loses sensitivity to the low-mass subhalos; with noise, the $10^{8.5}M_{\odot}$ subhalos are detected 86% of the time, but the $10^8 M_{\odot}$ subhalos are only detected 38% of the time. The false-positive rate is around 2 false subhalos per 100 images with and without noise, coming mostly from masses $\leq10^8 M_{\odot}$. With good accuracy and a low false-positive rate, counting the number of pixels assigned to each subhalo class over multiple images allows for a measurement of the subhalo mass function (SMF). When measured over five mass bins from $10^8 M_{\odot}$ to $10^{10} M_{\odot}$ the SMF slope is recovered with an error of 14.2 (16.3)% for 10 images, and this improves to 2.1 (2.6)% for 1000 images without (with 1%) noise.

Flow-Based Likelihoods for Non-Gaussian Inference

We investigate the use of data-driven likelihoods to bypass a key assumption made in many scientific analyses, which is that the true likelihood of the data is Gaussian. In particular, we suggest using the optimization targets of flow-based generative models, a class of models that can capture complex distributions by transforming a simple base distribution through layers of nonlinearities. We call these flow-based likelihoods (FBL). We analyze the accuracy and precision of the reconstructed likelihoods on mock Gaussian data, and show that simply gauging the quality of samples drawn from the trained model is not a sufficient indicator that the true likelihood has been learned. We nevertheless demonstrate that the likelihood can be reconstructed to a precision equal to that of sampling error due to a finite sample size. We then apply FBLs to mock weak lensing convergence power spectra, a cosmological observable that is significantly non-Gaussian (NG). We find that the FBL captures the NG signatures in the data extremely well, while other commonly-used data-driven likelihoods, such as Gaussian mixture models and independent component analysis, fail to do so. This suggests that works that have found small posterior shifts in NG data with data-driven likelihoods such as these could be underestimating the impact of non-Gaussianity in parameter constraints. By introducing a suite of tests that can capture different levels of NG in the data, we show that the success or failure of traditional data-driven likelihoods can be tied back to the structure of the NG in the data. Unlike other methods, the flexibility of the FBL makes it successful at tackling different types of NG simultaneously. Because of this, and consequently their likely applicability across datasets and domains, we encourage their use for inference when sufficient mock data are available for training.

A Novel CMB Component Separation Method: Hierarchical Generalized Morphological Component Analysis

We present a novel technique for Cosmic Microwave Background (CMB) foreground subtraction based on the framework of blind source separation. Inspired by previous work incorporating local variation to Generalized Morphological Component Analysis (GMCA), we introduce Hierarchical GMCA (HGMCA), a Bayesian hierarchical framework for source separation. We test our method on $N_{\rm side}=256$ simulated sky maps that include dust, synchrotron, free-free and anomalous microwave emission, and show that HGMCA reduces foreground contamination by $25\%$ over GMCA in both the regions included and excluded by the Planck UT78 mask, decreases the error in the measurement of the CMB temperature power spectrum to the $0.02-0.03\%$ level at $\ell>200$ (and $<0.26\%$ for all $\ell$), and reduces correlation to all the foregrounds. We find equivalent or improved performance when compared to state-of-the-art Internal Linear Combination (ILC)-type algorithms on these simulations, suggesting that HGMCA may be a competitive alternative to foreground separation techniques previously applied to observed CMB data. Additionally, we show that our performance does not suffer when we perturb model parameters or alter the CMB realization, which suggests that our algorithm generalizes well beyond our simplified simulations. Our results open a new avenue for constructing CMB maps through Bayesian hierarchical analysis.