Rule-based Evaluation and Optimal Control for Autonomous Driving

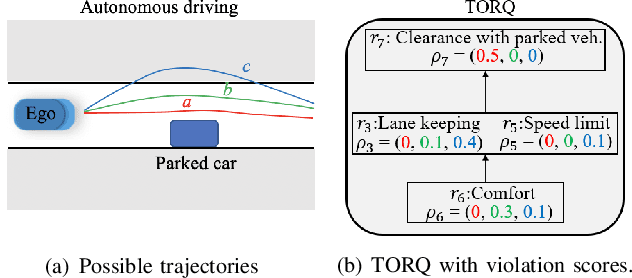
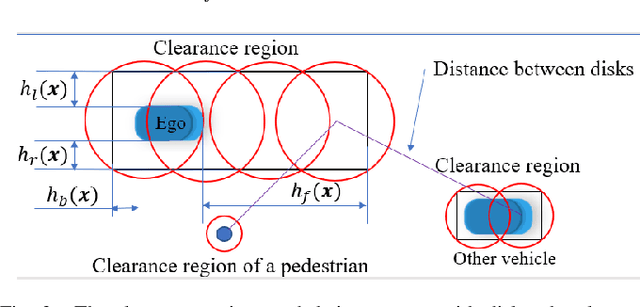
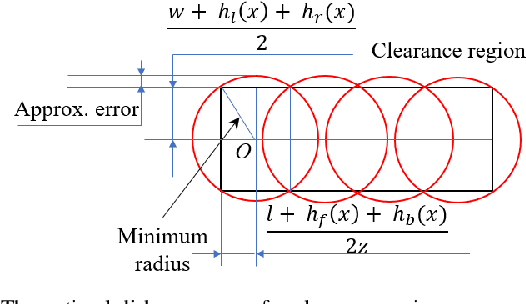
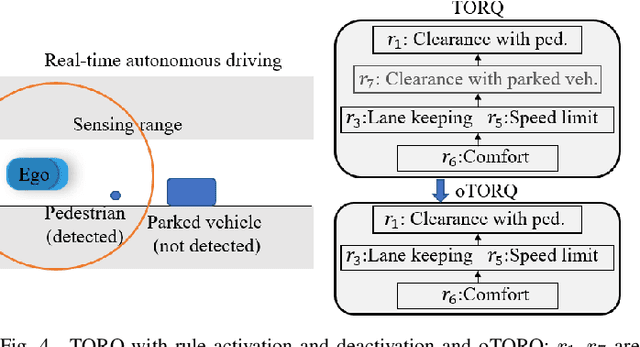
We develop optimal control strategies for autonomous vehicles (AVs) that are required to meet complex specifications imposed as rules of the road (ROTR) and locally specific cultural expectations of reasonable driving behavior. We formulate these specifications as rules, and specify their priorities by constructing a priority structure, called \underline{T}otal \underline{OR}der over e\underline{Q}uivalence classes (TORQ). We propose a recursive framework, in which the satisfaction of the rules in the priority structure are iteratively relaxed in reverse order of priority. Central to this framework is an optimal control problem, where convergence to desired states is achieved using Control Lyapunov Functions (CLFs) and clearance with other road users is enforced through Control Barrier Functions (CBFs). We present offline and online approaches to this problem. In the latter, the AV has limited sensing range that affects the activation of the rules, and the control is generated using a receding horizon (Model Predictive Control, MPC) approach. We also show how the offline method can be used for after-the-fact (offline) pass/fail evaluation of trajectories - a given trajectory is rejected if we can find a controller producing a trajectory that leads to less violation of the rule priority structure. We present case studies with multiple driving scenarios to demonstrate the effectiveness of the algorithms, and to compare the offline and online versions of our proposed framework.

Plane and Sample: Maximizing Information about Autonomous Vehicle Performance using Submodular Optimization

As autonomous vehicles (AVs) take on growing Operational Design Domains (ODDs), they need to go through a systematic, transparent, and scalable evaluation process to demonstrate their benefits to society. Current scenario sampling techniques for AV performance evaluation usually focus on a specific functionality, such as lane changing, and do not accommodate a transfer of information about an AV system from one ODD to the next. In this paper, we reformulate the scenario sampling problem across ODDs and functionalities as a submodular optimization problem. To do so, we abstract AV performance as a Bayesian Hierarchical Model, which we use to infer information gained by revealing performance in new scenarios. We propose the information gain as a measure of scenario relevance and evaluation progress. Furthermore, we leverage the submodularity, or diminishing returns, property of the information gain not only to find a near-optimal scenario set, but also to propose a stopping criterion for an AV performance evaluation campaign. We find that we only need to explore about 7.5% of the scenario space to meet this criterion, a 23% improvement over Latin Hypercube Sampling.