Fairness Under Group-Conditional Prior Probability Shift: Invariance, Drift, and Target-Aware Post-Processing

Machine learning systems are often trained and evaluated for fairness on historical data, yet deployed in environments where conditions have shifted. A particularly common form of shift occurs when the prevalence of positive outcomes changes differently across demographic groups--for example, when disease rates rise faster in one population than another, or when economic conditions affect loan default rates unequally. We study group-conditional prior probability shift (GPPS), where the label prevalence $P(Y=1\mid A=a)$ may change between training and deployment while the feature-generation process $P(X\mid Y,A)$ remains stable. Our analysis yields three main contributions. First, we prove a fundamental dichotomy: fairness criteria based on error rates (equalized odds) are structurally invariant under GPPS, while acceptance-rate criteria (demographic parity) can drift--and we prove this drift is unavoidable for non-trivial classifiers (shift-robust impossibility). Second, we show that target-domain risk and fairness metrics are identifiable without target labels: the invariance of ROC quantities under GPPS enables consistent estimation from source labels and unlabeled target data alone, with finite-sample guarantees. Third, we propose TAP-GPPS, a label-free post-processing algorithm that estimates prevalences from unlabeled data, corrects posteriors, and selects thresholds to satisfy demographic parity in the target domain. Experiments validate our theoretical predictions and demonstrate that TAP-GPPS achieves target fairness with minimal utility loss.

Fix Representation (Optimally) Before Fairness: Finite-Sample Shrinkage Population Correction and the True Price of Fairness Under Subpopulation Shift

Machine learning practitioners frequently observe tension between predictive accuracy and group fairness constraints -- yet sometimes fairness interventions appear to improve accuracy. We show that both phenomena can be artifacts of training data that misrepresents subgroup proportions. Under subpopulation shift (stable within-group distributions, shifted group proportions), we establish: (i) full importance-weighted correction is asymptotically unbiased but finite-sample suboptimal; (ii) the optimal finite-sample correction is a shrinkage reweighting that interpolates between target and training mixtures; (iii) apparent "fairness helps accuracy" can arise from comparing fairness methods to an improperly-weighted baseline. We provide an actionable evaluation protocol: fix representation (optimally) before fairness -- compare fairness interventions against a shrinkage-corrected baseline to isolate the true, irreducible price of fairness. Experiments on synthetic and real-world benchmarks (Adult, COMPAS) validate our theoretical predictions and demonstrate that this protocol eliminates spurious tradeoffs, revealing the genuine fairness-utility frontier.

Projected Boosting with Fairness Constraints: Quantifying the Cost of Fair Training Distributions

Boosting algorithms enjoy strong theoretical guarantees: when weak learners maintain positive edge, AdaBoost achieves geometric decrease of exponential loss. We study how to incorporate group fairness constraints into boosting while preserving analyzable training dynamics. Our approach, FairBoost, projects the ensemble-induced exponential-weights distribution onto a convex set of distributions satisfying fairness constraints (as a reweighting surrogate), then trains weak learners on this fair distribution. The key theoretical insight is that projecting the training distribution reduces the effective edge of weak learners by a quantity controlled by the KL-divergence of the projection. We prove an exponential-loss bound where the convergence rate depends on weak learner edge minus a "fairness cost" term $δ_t = \sqrt{\mathrm{KL}(w^t \| q^t)/2}$. This directly quantifies the accuracy-fairness tradeoff in boosting dynamics. Experiments on standard benchmarks validate the theoretical predictions and demonstrate competitive fairness-accuracy tradeoffs with stable training curves.

Causal Discovery with Mixed Latent Confounding via Precision Decomposition

We study causal discovery from observational data in linear Gaussian systems affected by \emph{mixed latent confounding}, where some unobserved factors act broadly across many variables while others influence only small subsets. This setting is common in practice and poses a challenge for existing methods: differentiable and score-based DAG learners can misinterpret global latent effects as causal edges, while latent-variable graphical models recover only undirected structure. We propose \textsc{DCL-DECOR}, a modular, precision-led pipeline that separates these roles. The method first isolates pervasive latent effects by decomposing the observed precision matrix into a structured component and a low-rank component. The structured component corresponds to the conditional distribution after accounting for pervasive confounders and retains only local dependence induced by the causal graph and localized confounding. A correlated-noise DAG learner is then applied to this deconfounded representation to recover directed edges while modeling remaining structured error correlations, followed by a simple reconciliation step to enforce bow-freeness. We provide identifiability results that characterize the recoverable causal target under mixed confounding and show how the overall problem reduces to well-studied subproblems with modular guarantees. Synthetic experiments that vary the strength and dimensionality of pervasive confounding demonstrate consistent improvements in directed edge recovery over applying correlated-noise DAG learning directly to the confounded data.

DAG DECORation: Continuous Optimization for Structure Learning under Hidden Confounding

We study structure learning for linear Gaussian SEMs in the presence of latent confounding. Existing continuous methods excel when errors are independent, while deconfounding-first pipelines rely on pervasive factor structure or nonlinearity. We propose \textsc{DECOR}, a single likelihood-based and fully differentiable estimator that jointly learns a DAG and a correlated noise model. Our theory gives simple sufficient conditions for global parameter identifiability: if the mixed graph is bow free and the noise covariance has a uniform eigenvalue margin, then the map from $(\B,\OmegaMat)$ to the observational covariance is injective, so both the directed structure and the noise are uniquely determined. The estimator alternates a smooth-acyclic graph update with a convex noise update and can include a light bow complementarity penalty or a post hoc reconciliation step. On synthetic benchmarks that vary confounding density, graph density, latent rank, and dimension with $n<p$, \textsc{DECOR} matches or outperforms strong baselines and is especially robust when confounding is non-pervasive, while remaining competitive under pervasiveness.

Time Series Deinterleaving of DNS Traffic

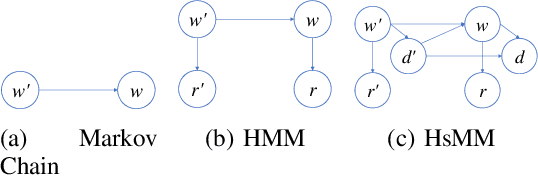
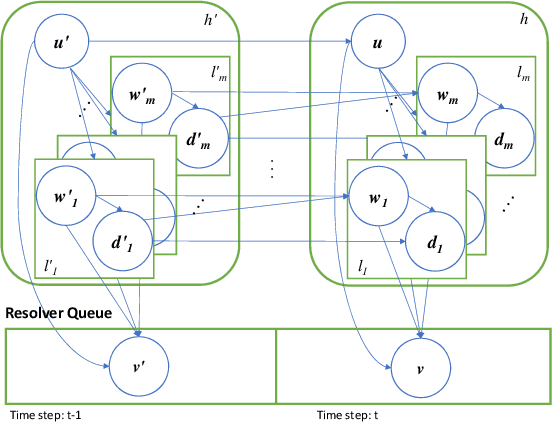
Stream deinterleaving is an important problem with various applications in the cybersecurity domain. In this paper, we consider the specific problem of deinterleaving DNS data streams using machine-learning techniques, with the objective of automating the extraction of malware domain sequences. We first develop a generative model for user request generation and DNS stream interleaving. Based on these we evaluate various inference strategies for deinterleaving including augmented HMMs and LSTMs on synthetic datasets. Our results demonstrate that state-of-the-art LSTMs outperform more traditional augmented HMMs in this application domain.

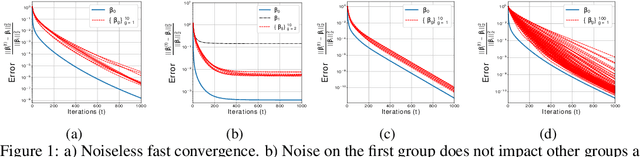
High Dimensional Data Enrichment: Interpretable, Fast, and Data-Efficient

High dimensional structured data enriched model describes groups of observations by shared and per-group individual parameters, each with its own structure such as sparsity or group sparsity. In this paper, we consider the general form of data enrichment where data comes in a fixed but arbitrary number of groups G. Any convex function, e.g., norms, can characterize the structure of both shared and individual parameters. We propose an estimator for high dimensional data enriched model and provide conditions under which it consistently estimates both shared and individual parameters. We also delineate sample complexity of the estimator and present high probability non-asymptotic bound on estimation error of all parameters. Interestingly the sample complexity of our estimator translates to conditions on both per-group sample sizes and the total number of samples. We propose an iterative estimation algorithm with linear convergence rate and supplement our theoretical analysis with synthetic and real experimental results. Particularly, we show the predictive power of data-enriched model along with its interpretable results in anticancer drug sensitivity analysis.