Partial Models for Building Adaptive Model-Based Reinforcement Learning Agents

In neuroscience, one of the key behavioral tests for determining whether a subject of study exhibits model-based behavior is to study its adaptiveness to local changes in the environment. In reinforcement learning, however, recent studies have shown that modern model-based agents display poor adaptivity to such changes. The main reason for this is that modern agents are typically designed to improve sample efficiency in single task settings and thus do not take into account the challenges that can arise in other settings. In local adaptation settings, one particularly important challenge is in quickly building and maintaining a sufficiently accurate model after a local change. This is challenging for deep model-based agents as their models and replay buffers are monolithic structures lacking distribution shift handling capabilities. In this study, we show that the conceptually simple idea of partial models can allow deep model-based agents to overcome this challenge and thus allow for building locally adaptive model-based agents. By modeling the different parts of the state space through different models, the agent can not only maintain a model that is accurate across the state space, but it can also quickly adapt it in the presence of a local change in the environment. We demonstrate this by showing that the use of partial models in agents such as deep Dyna-Q, PlaNet and Dreamer can allow for them to effectively adapt to the local changes in their environments.

Replay Buffer With Local Forgetting for Adaptive Deep Model-Based Reinforcement Learning

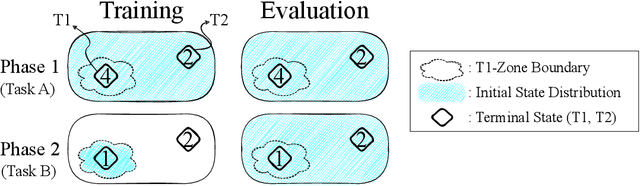
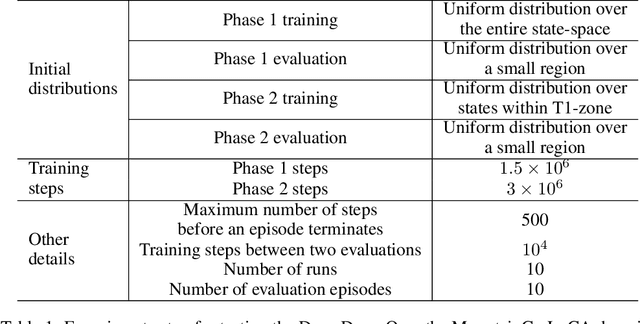
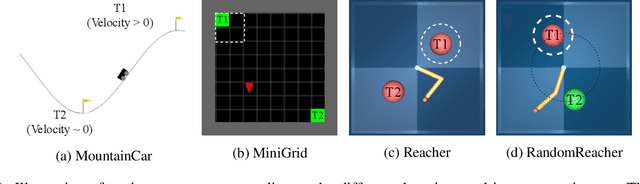
One of the key behavioral characteristics used in neuroscience to determine whether the subject of study -- be it a rodent or a human -- exhibits model-based learning is effective adaptation to local changes in the environment. In reinforcement learning, however, recent work has shown that modern deep model-based reinforcement-learning (MBRL) methods adapt poorly to such changes. An explanation for this mismatch is that MBRL methods are typically designed with sample-efficiency on a single task in mind and the requirements for effective adaptation are substantially higher, both in terms of the learned world model and the planning routine. One particularly challenging requirement is that the learned world model has to be sufficiently accurate throughout relevant parts of the state-space. This is challenging for deep-learning-based world models due to catastrophic forgetting. And while a replay buffer can mitigate the effects of catastrophic forgetting, the traditional first-in-first-out replay buffer precludes effective adaptation due to maintaining stale data. In this work, we show that a conceptually simple variation of this traditional replay buffer is able to overcome this limitation. By removing only samples from the buffer from the local neighbourhood of the newly observed samples, deep world models can be built that maintain their accuracy across the state-space, while also being able to effectively adapt to changes in the reward function. We demonstrate this by applying our replay-buffer variation to a deep version of the classical Dyna method, as well as to recent methods such as PlaNet and DreamerV2, demonstrating that deep model-based methods can adapt effectively as well to local changes in the environment.

Towards Evaluating Adaptivity of Model-Based Reinforcement Learning Methods

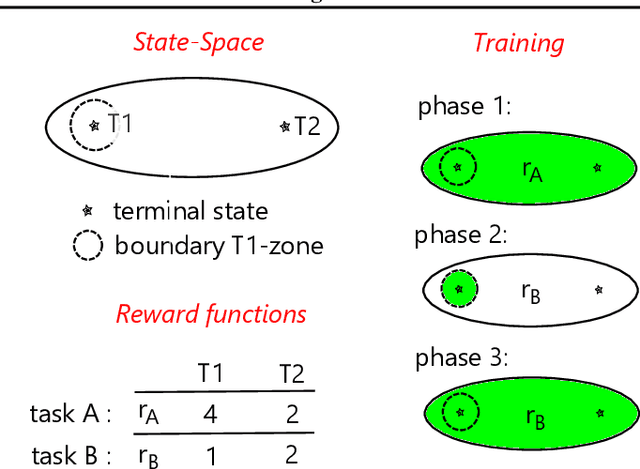
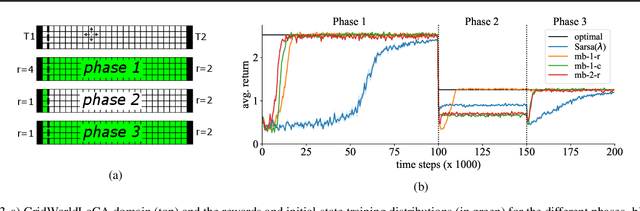
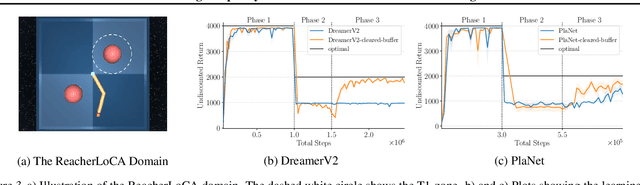
In recent years, a growing number of deep model-based reinforcement learning (RL) methods have been introduced. The interest in deep model-based RL is not surprising, given its many potential benefits, such as higher sample efficiency and the potential for fast adaption to changes in the environment. However, we demonstrate, using an improved version of the recently introduced Local Change Adaptation (LoCA) setup, that well-known model-based methods such as PlaNet and DreamerV2 perform poorly in their ability to adapt to local environmental changes. Combined with prior work that made a similar observation about the other popular model-based method, MuZero, a trend appears to emerge, suggesting that current deep model-based methods have serious limitations. We dive deeper into the causes of this poor performance, by identifying elements that hurt adaptive behavior and linking these to underlying techniques frequently used in deep model-based RL. We empirically validate these insights in the case of linear function approximation by demonstrating that a modified version of linear Dyna achieves effective adaptation to local changes. Furthermore, we provide detailed insights into the challenges of building an adaptive nonlinear model-based method, by experimenting with a nonlinear version of Dyna.