Hybrid Forecasting of Geopolitical Events

Sound decision-making relies on accurate prediction for tangible outcomes ranging from military conflict to disease outbreaks. To improve crowdsourced forecasting accuracy, we developed SAGE, a hybrid forecasting system that combines human and machine generated forecasts. The system provides a platform where users can interact with machine models and thus anchor their judgments on an objective benchmark. The system also aggregates human and machine forecasts weighting both for propinquity and based on assessed skill while adjusting for overconfidence. We present results from the Hybrid Forecasting Competition (HFC) - larger than comparable forecasting tournaments - including 1085 users forecasting 398 real-world forecasting problems over eight months. Our main result is that the hybrid system generated more accurate forecasts compared to a human-only baseline which had no machine generated predictions. We found that skilled forecasters who had access to machine-generated forecasts outperformed those who only viewed historical data. We also demonstrated the inclusion of machine-generated forecasts in our aggregation algorithms improved performance, both in terms of accuracy and scalability. This suggests that hybrid forecasting systems, which potentially require fewer human resources, can be a viable approach for maintaining a competitive level of accuracy over a larger number of forecasting questions.

An information theory for preferences

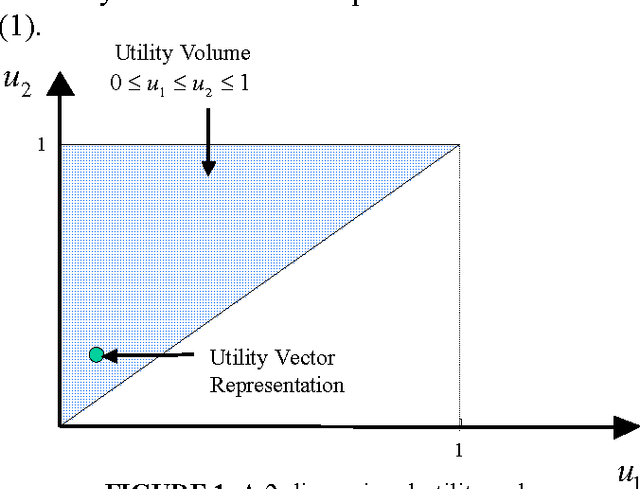
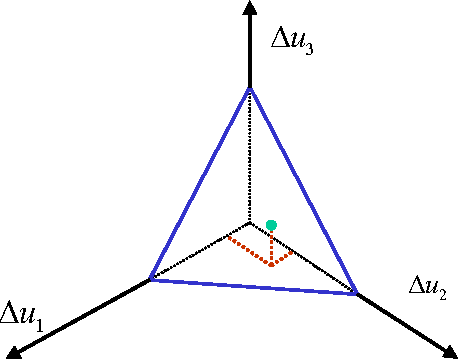
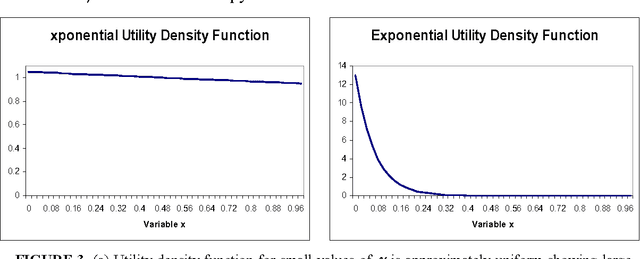
Recent literature in the last Maximum Entropy workshop introduced an analogy between cumulative probability distributions and normalized utility functions. Based on this analogy, a utility density function can de defined as the derivative of a normalized utility function. A utility density function is non-negative and integrates to unity. These two properties form the basis of a correspondence between utility and probability. A natural application of this analogy is a maximum entropy principle to assign maximum entropy utility values. Maximum entropy utility interprets many of the common utility functions based on the preference information needed for their assignment, and helps assign utility values based on partial preference information. This paper reviews maximum entropy utility and introduces further results that stem from the duality between probability and utility.

The Algebra of Utility Inference

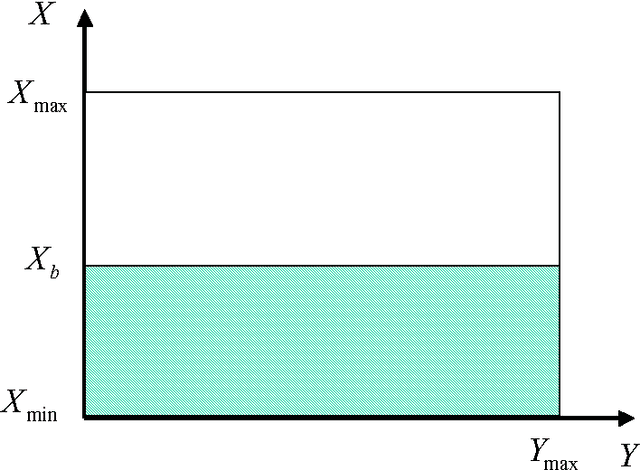
Richard Cox [1] set the axiomatic foundations of probable inference and the algebra of propositions. He showed that consistency within these axioms requires certain rules for updating belief. In this paper we use the analogy between probability and utility introduced in [2] to propose an axiomatic foundation for utility inference and the algebra of preferences. We show that consistency within these axioms requires certain rules for updating preference. We discuss a class of utility functions that stems from the axioms of utility inference and show that this class is the basic building block for any general multiattribute utility function. We use this class of utility functions together with the algebra of preferences to construct utility functions represented by logical operations on the attributes.