An information theory for preferences

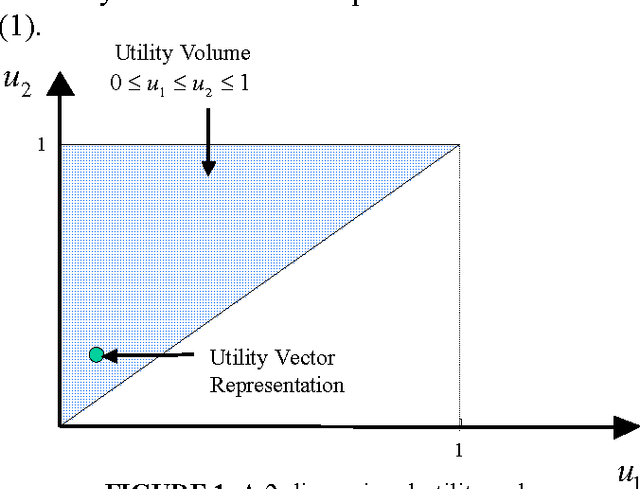
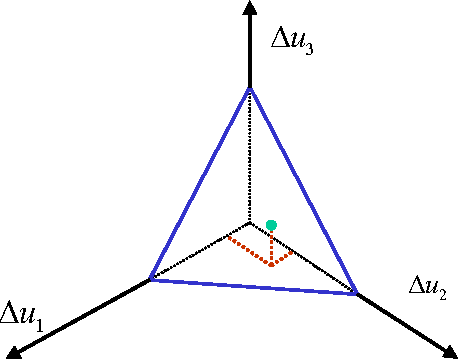
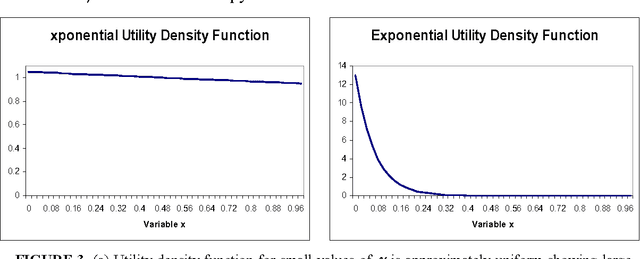
Recent literature in the last Maximum Entropy workshop introduced an analogy between cumulative probability distributions and normalized utility functions. Based on this analogy, a utility density function can de defined as the derivative of a normalized utility function. A utility density function is non-negative and integrates to unity. These two properties form the basis of a correspondence between utility and probability. A natural application of this analogy is a maximum entropy principle to assign maximum entropy utility values. Maximum entropy utility interprets many of the common utility functions based on the preference information needed for their assignment, and helps assign utility values based on partial preference information. This paper reviews maximum entropy utility and introduces further results that stem from the duality between probability and utility.