Alexis Linard
Robust MITL planning under uncertain navigation times
Mar 06, 2024



Abstract:In environments like offices, the duration of a robot's navigation between two locations may vary over time. For instance, reaching a kitchen may take more time during lunchtime since the corridors are crowded with people heading the same way. In this work, we address the problem of routing in such environments with tasks expressed in Metric Interval Temporal Logic (MITL) - a rich robot task specification language that allows us to capture explicit time requirements. Our objective is to find a strategy that maximizes the temporal robustness of the robot's MITL task. As the first step towards a solution, we define a Mixed-integer linear programming approach to solving the task planning problem over a Varying Weighted Transition System, where navigation durations are deterministic but vary depending on the time of day. Then, we apply this planner to optimize for MITL temporal robustness in Markov Decision Processes, where the navigation durations between physical locations are uncertain, but the time-dependent distribution over possible delays is known. Finally, we develop a receding horizon planner for Markov Decision Processes that preserves guarantees over MITL temporal robustness. We show the scalability of our planning algorithms in simulations of robotic tasks.
Learning Pairwise Disjoint Simple Languages from Positive Examples
Jun 06, 2017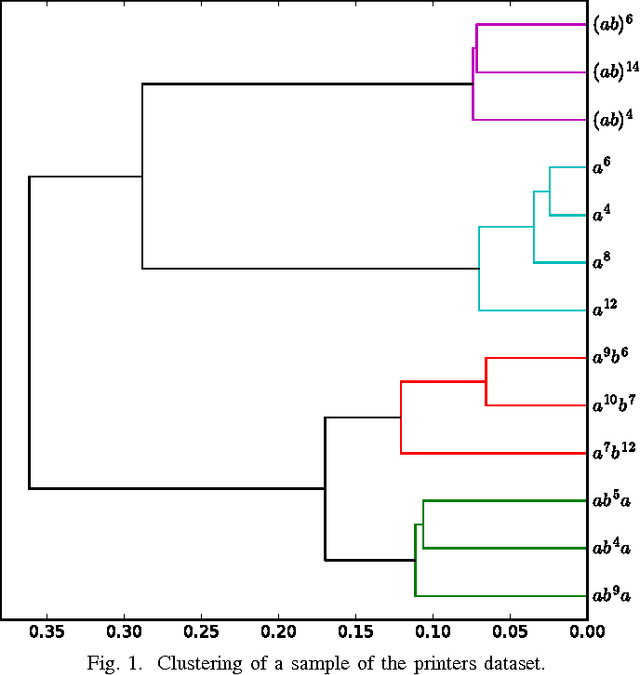


Abstract:A classical problem in grammatical inference is to identify a deterministic finite automaton (DFA) from a set of positive and negative examples. In this paper, we address the related - yet seemingly novel - problem of identifying a set of DFAs from examples that belong to different unknown simple regular languages. We propose two methods based on compression for clustering the observed positive examples. We apply our methods to a set of print jobs submitted to large industrial printers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge