Learning Pairwise Disjoint Simple Languages from Positive Examples

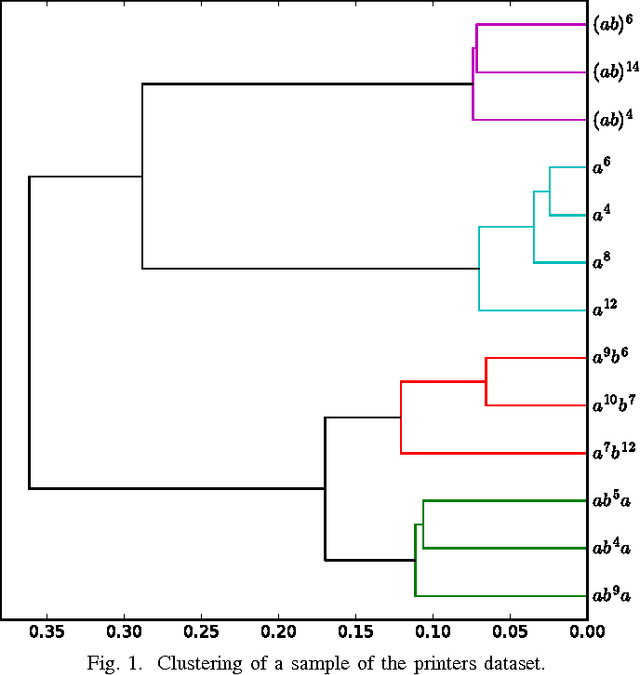
A classical problem in grammatical inference is to identify a deterministic finite automaton (DFA) from a set of positive and negative examples. In this paper, we address the related - yet seemingly novel - problem of identifying a set of DFAs from examples that belong to different unknown simple regular languages. We propose two methods based on compression for clustering the observed positive examples. We apply our methods to a set of print jobs submitted to large industrial printers.

Grammatical Inference as a Satisfiability Modulo Theories Problem

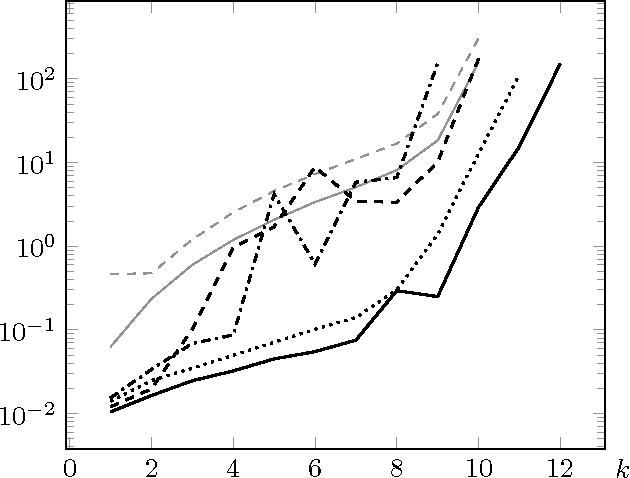
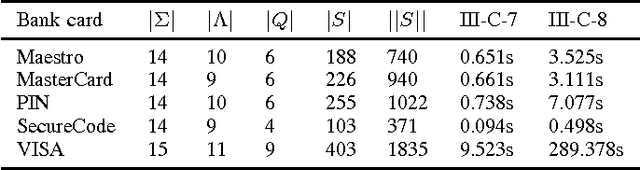
The problem of learning a minimal consistent model from a set of labeled sequences of symbols is addressed from a satisfiability modulo theories perspective. We present two encodings for deterministic finite automata and extend one of these for Moore and Mealy machines. Our experimental results show that these encodings improve upon the state-of-the-art, and are useful in practice for learning small models.