Grammatical Inference as a Satisfiability Modulo Theories Problem
Paper and Code
May 30, 2017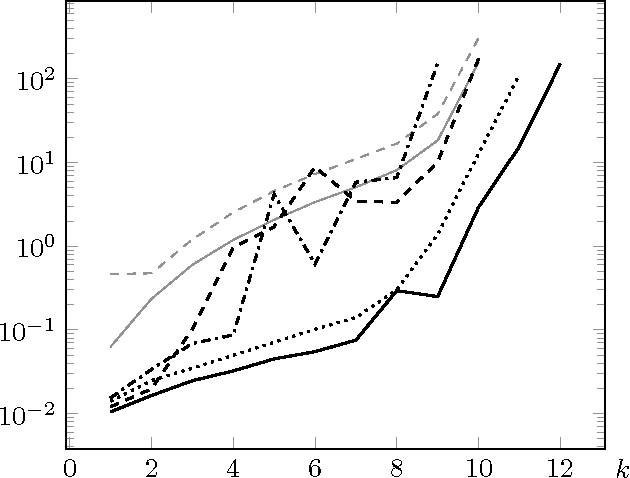
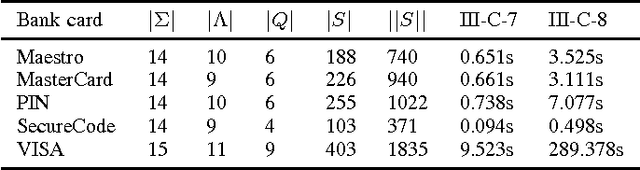
The problem of learning a minimal consistent model from a set of labeled sequences of symbols is addressed from a satisfiability modulo theories perspective. We present two encodings for deterministic finite automata and extend one of these for Moore and Mealy machines. Our experimental results show that these encodings improve upon the state-of-the-art, and are useful in practice for learning small models.
* Submitted and selected for oral presentation at the LearnAut workshop
at LICS 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge