Markov Chain Analysis of Evolution Strategies on a Linear Constraint Optimization Problem

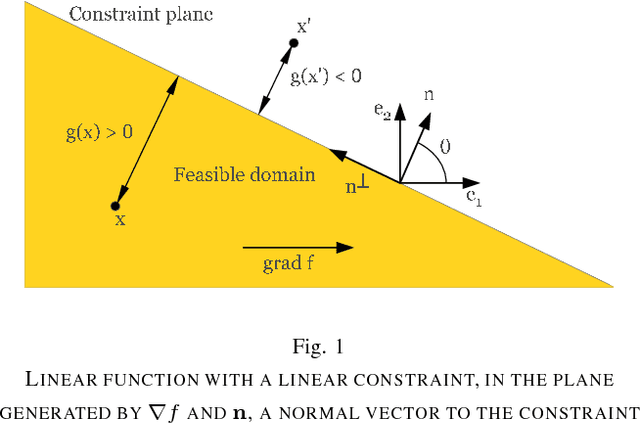
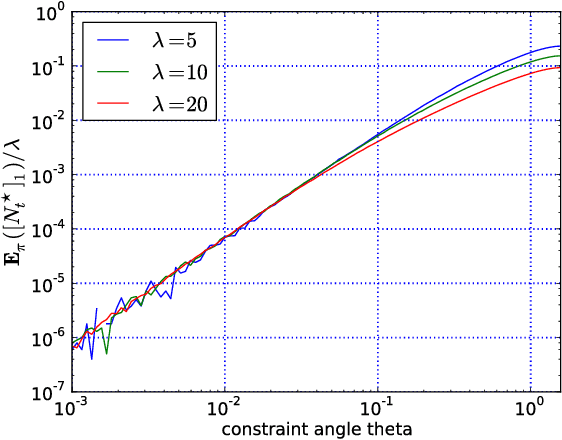
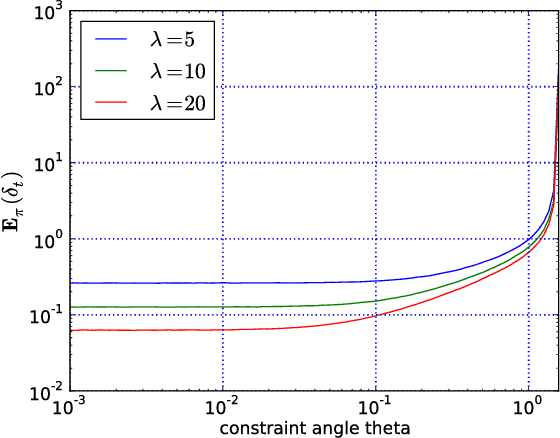
This paper analyses a $(1,\lambda)$-Evolution Strategy, a randomised comparison-based adaptive search algorithm, on a simple constraint optimisation problem. The algorithm uses resampling to handle the constraint and optimizes a linear function with a linear constraint. Two cases are investigated: first the case where the step-size is constant, and second the case where the step-size is adapted using path length control. We exhibit for each case a Markov chain whose stability analysis would allow us to deduce the divergence of the algorithm depending on its internal parameters. We show divergence at a constant rate when the step-size is constant. We sketch that with step-size adaptation geometric divergence takes place. Our results complement previous studies where stability was assumed.

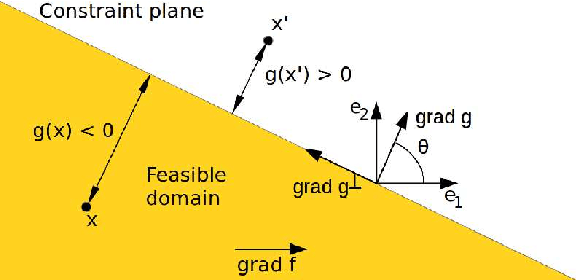
A Generalized Markov-Chain Modelling Approach to $(1,λ)$-ES Linear Optimization: Technical Report

Several recent publications investigated Markov-chain modelling of linear optimization by a $(1,\lambda)$-ES, considering both unconstrained and linearly constrained optimization, and both constant and varying step size. All of them assume normality of the involved random steps, and while this is consistent with a black-box scenario, information on the function to be optimized (e.g. separability) may be exploited by the use of another distribution. The objective of our contribution is to complement previous studies realized with normal steps, and to give sufficient conditions on the distribution of the random steps for the success of a constant step-size $(1,\lambda)$-ES on the simple problem of a linear function with a linear constraint. The decomposition of a multidimensional distribution into its marginals and the copula combining them is applied to the new distributional assumptions, particular attention being paid to distributions with Archimedean copulas.

Cumulative Step-size Adaptation on Linear Functions

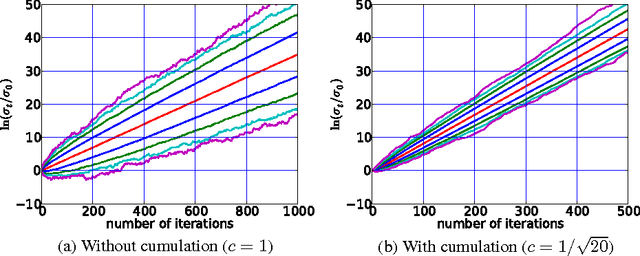
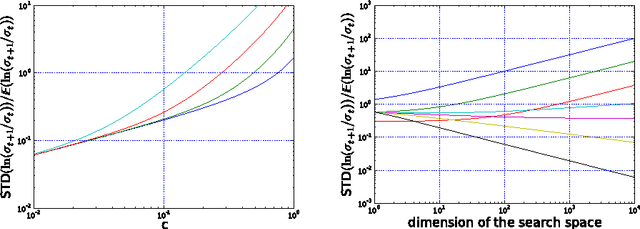
The CSA-ES is an Evolution Strategy with Cumulative Step size Adaptation, where the step size is adapted measuring the length of a so-called cumulative path. The cumulative path is a combination of the previous steps realized by the algorithm, where the importance of each step decreases with time. This article studies the CSA-ES on composites of strictly increasing functions with affine linear functions through the investigation of its underlying Markov chains. Rigorous results on the change and the variation of the step size are derived with and without cumulation. The step-size diverges geometrically fast in most cases. Furthermore, the influence of the cumulation parameter is studied.