Cumulative Step-size Adaptation on Linear Functions
Paper and Code
Dec 01, 2012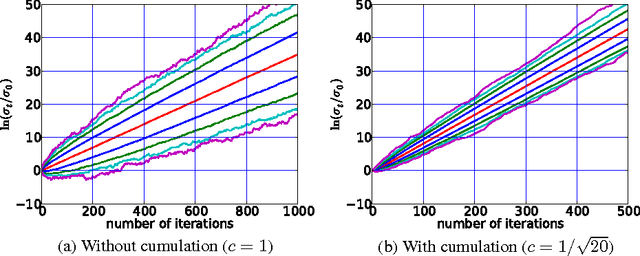
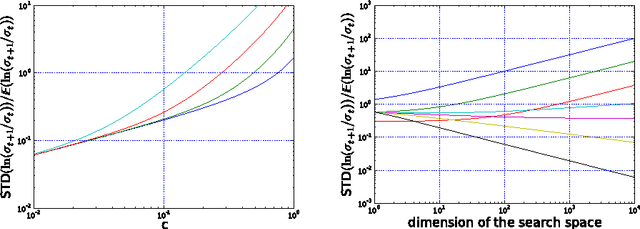
The CSA-ES is an Evolution Strategy with Cumulative Step size Adaptation, where the step size is adapted measuring the length of a so-called cumulative path. The cumulative path is a combination of the previous steps realized by the algorithm, where the importance of each step decreases with time. This article studies the CSA-ES on composites of strictly increasing functions with affine linear functions through the investigation of its underlying Markov chains. Rigorous results on the change and the variation of the step size are derived with and without cumulation. The step-size diverges geometrically fast in most cases. Furthermore, the influence of the cumulation parameter is studied.
* PPSN 2012 (2012) 72-81 * arXiv admin note: substantial text overlap with arXiv:1206.1208
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge