Adaptive Generation-Based Evolution Control for Gaussian Process Surrogate Models

The interest in accelerating black-box optimizers has resulted in several surrogate model-assisted version of the Covariance Matrix Adaptation Evolution Strategy, a state-of-the-art continuous black-box optimizer. The version called Surrogate CMA-ES uses Gaussian processes or random forests surrogate models with a generation-based evolution control. This paper presents an adaptive improvement for S-CMA-ES based on a general procedure introduced with the s*ACM-ES algorithm, in which the number of generations using the surrogate model before retraining is adjusted depending on the performance of the last instance of the surrogate. Three algorithms that differ in the measure of the surrogate model's performance are evaluated on the COCO/BBOB framework. The results show a minor improvement on S-CMA-ES with constant model lifelengths, especially when larger lifelengths are considered.

Model Guided Sampling Optimization for Low-dimensional Problems

Optimization of very expensive black-box functions requires utilization of maximum information gathered by the process of optimization. Model Guided Sampling Optimization (MGSO) forms a more robust alternative to Jones' Gaussian-process-based EGO algorithm. Instead of EGO's maximizing expected improvement, the MGSO uses sampling the probability of improvement which is shown to be helpful against trapping in local minima. Further, the MGSO can reach close-to-optimum solutions faster than standard optimization algorithms on low dimensional or smooth problems.

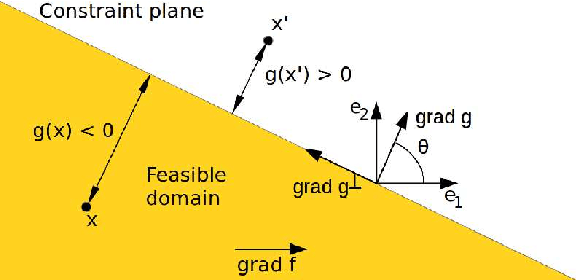
A Generalized Markov-Chain Modelling Approach to $(1,λ)$-ES Linear Optimization: Technical Report

Several recent publications investigated Markov-chain modelling of linear optimization by a $(1,\lambda)$-ES, considering both unconstrained and linearly constrained optimization, and both constant and varying step size. All of them assume normality of the involved random steps, and while this is consistent with a black-box scenario, information on the function to be optimized (e.g. separability) may be exploited by the use of another distribution. The objective of our contribution is to complement previous studies realized with normal steps, and to give sufficient conditions on the distribution of the random steps for the success of a constant step-size $(1,\lambda)$-ES on the simple problem of a linear function with a linear constraint. The decomposition of a multidimensional distribution into its marginals and the copula combining them is applied to the new distributional assumptions, particular attention being paid to distributions with Archimedean copulas.