Receding Horizon Re-ordering of Multi-Agent Execution Schedules

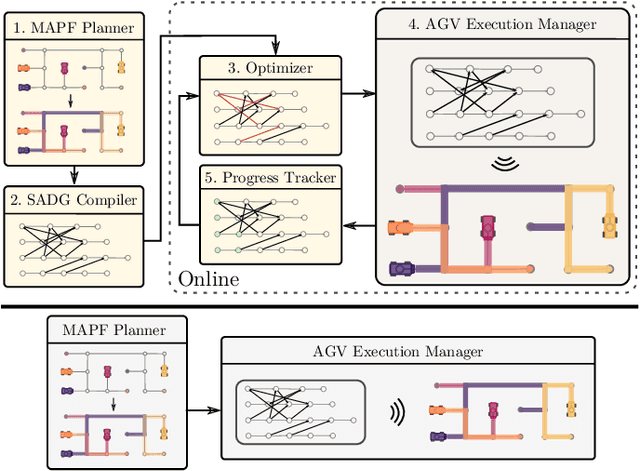
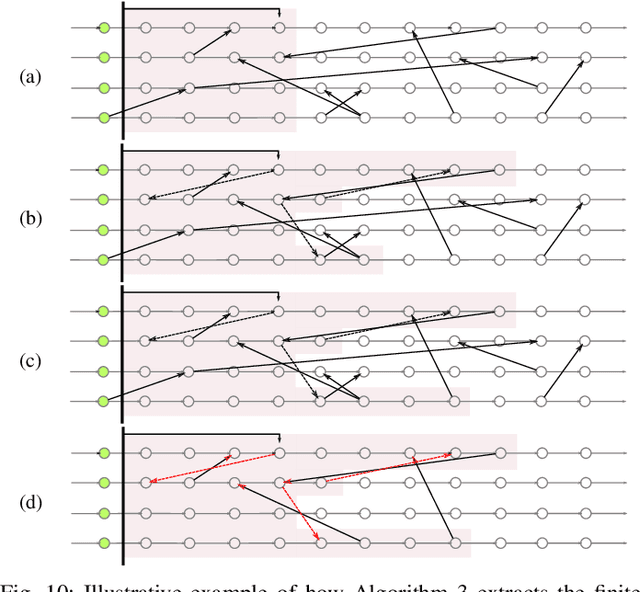
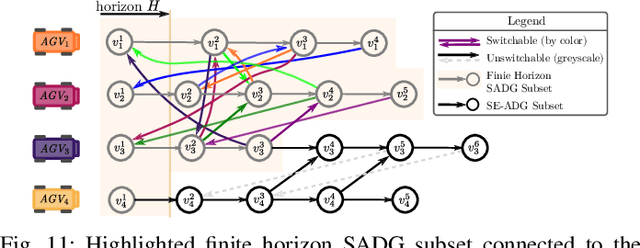
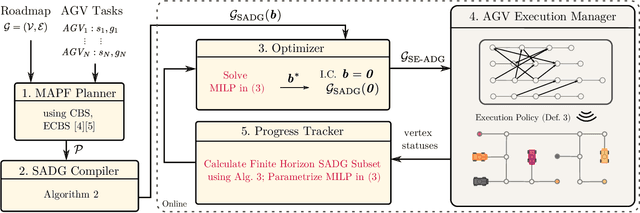
The trajectory planning for a fleet of Automated Guided Vehicles (AGVs) on a roadmap is commonly referred to as the Multi-Agent Path Finding (MAPF) problem, the solution to which dictates each AGV's spatial and temporal location until it reaches it's goal without collision. When executing MAPF plans in dynamic workspaces, AGVs can be frequently delayed, e.g., due to encounters with humans or third-party vehicles. If the remainder of the AGVs keeps following their individual plans, synchrony of the fleet is lost and some AGVs may pass through roadmap intersections in a different order than originally planned. Although this could reduce the cumulative route completion time of the AGVs, generally, a change in the original ordering can cause conflicts such as deadlocks. In practice, synchrony is therefore often enforced by using a MAPF execution policy employing, e.g., an Action Dependency Graph (ADG) to maintain ordering. To safely re-order without introducing deadlocks, we present the concept of the Switchable Action Dependency Graph (SADG). Using the SADG, we formulate a comparatively low-dimensional Mixed-Integer Linear Program (MILP) that repeatedly re-orders AGVs in a recursively feasible manner, thus maintaining deadlock-free guarantees, while dynamically minimizing the cumulative route completion time of all AGVs. Various simulations validate the efficiency of our approach when compared to the original ADG method as well as robust MAPF solution approaches.

A Feedback Scheme to Reorder a Multi-Agent Execution Schedule by Persistently Optimizing a Switchable Action Dependency Graph

In this paper we consider multiple Automated Guided Vehicles (AGVs) navigating a common workspace to fulfill various intralogistics tasks, typically formulated as the Multi-Agent Path Finding (MAPF) problem. To keep plan execution deadlock-free, one approach is to construct an Action Dependency Graph (ADG) which encodes the ordering of AGVs as they proceed along their routes. Using this method, delayed AGVs occasionally require others to wait for them at intersections, thereby affecting the plan execution efficiency. If the workspace is shared by dynamic obstacles such as humans or third party robots, AGVs can experience large delays. A common mitigation approach is to re-solve the MAPF using the current, delayed AGV positions. However, solving the MAPF is time-consuming, making this approach inefficient, especially for large AGV teams. In this work, we present an online method to repeatedly modify a given acyclic ADG to minimize route completion times of each AGV. Our approach persistently maintains an acyclic ADG, necessary for deadlock-free plan execution. We evaluate the approach by considering simulations with random disturbances on the execution and show faster route completion times compared to the baseline ADG-based execution management approach.