Alessandra Tosi
Distribution of Gaussian Process Arc Lengths
Mar 23, 2017
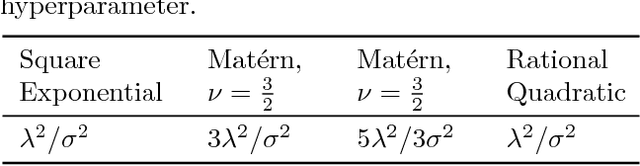
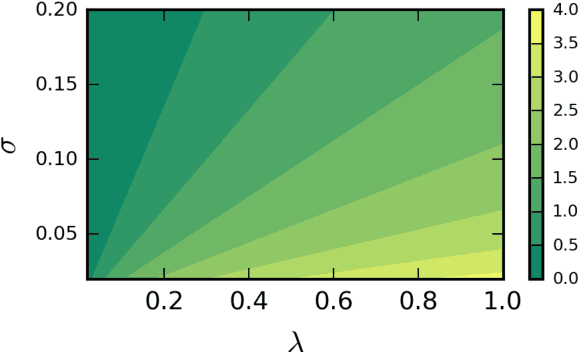

Abstract:We present the first treatment of the arc length of the Gaussian Process (GP) with more than a single output dimension. GPs are commonly used for tasks such as trajectory modelling, where path length is a crucial quantity of interest. Previously, only paths in one dimension have been considered, with no theoretical consideration of higher dimensional problems. We fill the gap in the existing literature by deriving the moments of the arc length for a stationary GP with multiple output dimensions. A new method is used to derive the mean of a one-dimensional GP over a finite interval, by considering the distribution of the arc length integrand. This technique is used to derive an approximate distribution over the arc length of a vector valued GP in $\mathbb{R}^n$ by moment matching the distribution. Numerical simulations confirm our theoretical derivations.
Metrics for Probabilistic Geometries
Nov 27, 2014



Abstract:We investigate the geometrical structure of probabilistic generative dimensionality reduction models using the tools of Riemannian geometry. We explicitly define a distribution over the natural metric given by the models. We provide the necessary algorithms to compute expected metric tensors where the distribution over mappings is given by a Gaussian process. We treat the corresponding latent variable model as a Riemannian manifold and we use the expectation of the metric under the Gaussian process prior to define interpolating paths and measure distance between latent points. We show how distances that respect the expected metric lead to more appropriate generation of new data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge