Justin D. Bewsher
Distribution of Gaussian Process Arc Lengths
Mar 23, 2017
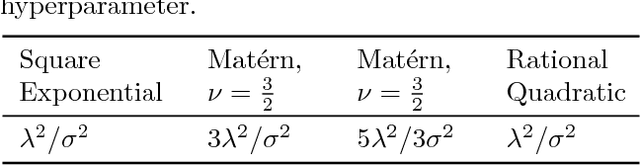

Abstract:We present the first treatment of the arc length of the Gaussian Process (GP) with more than a single output dimension. GPs are commonly used for tasks such as trajectory modelling, where path length is a crucial quantity of interest. Previously, only paths in one dimension have been considered, with no theoretical consideration of higher dimensional problems. We fill the gap in the existing literature by deriving the moments of the arc length for a stationary GP with multiple output dimensions. A new method is used to derive the mean of a one-dimensional GP over a finite interval, by considering the distribution of the arc length integrand. This technique is used to derive an approximate distribution over the arc length of a vector valued GP in $\mathbb{R}^n$ by moment matching the distribution. Numerical simulations confirm our theoretical derivations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge