Quality control for more reliable integration of deep learning-based image segmentation into medical workflows

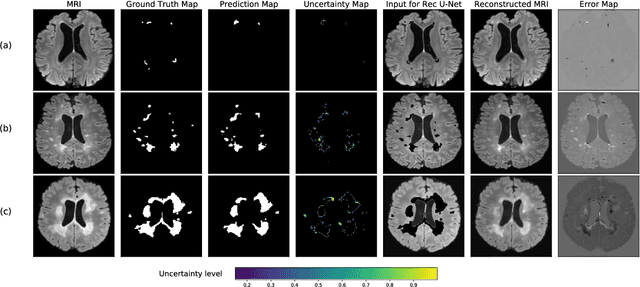
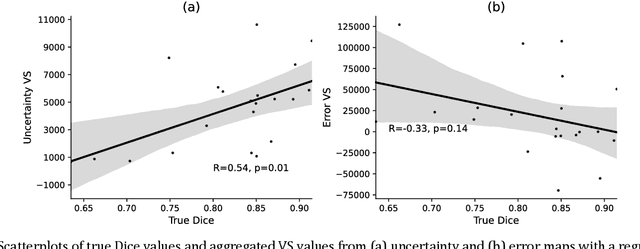
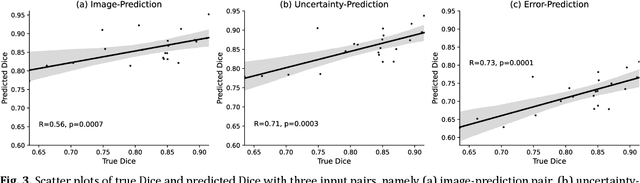
Machine learning algorithms underpin modern diagnostic-aiding software, which has proved valuable in clinical practice, particularly in radiology. However, inaccuracies, mainly due to the limited availability of clinical samples for training these algorithms, hamper their wider applicability, acceptance, and recognition amongst clinicians. We present an analysis of state-of-the-art automatic quality control (QC) approaches that can be implemented within these algorithms to estimate the certainty of their outputs. We validated the most promising approaches on a brain image segmentation task identifying white matter hyperintensities (WMH) in magnetic resonance imaging data. WMH are a correlate of small vessel disease common in mid-to-late adulthood and are particularly challenging to segment due to their varied size, and distributional patterns. Our results show that the aggregation of uncertainty and Dice prediction were most effective in failure detection for this task. Both methods independently improved mean Dice from 0.82 to 0.84. Our work reveals how QC methods can help to detect failed segmentation cases and therefore make automatic segmentation more reliable and suitable for clinical practice.

Convolutional neural network stacking for medical image segmentation in CT scans

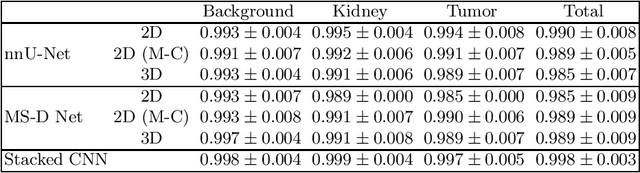
Computed tomography (CT) data poses many challenges to medical image segmentation based on convolutional neural networks(CNNs). The main challenges in handling CT scans with CNN are the scale of data (large range of Hounsfield Units) and the processing of the slices. In this paper, we consider a framework, which addresses these demands regarding the data pre-processing, the data augmentation, and the CNN architecture itself. For this purpose, we present a data preprocessing and an augmentation method tailored to CT data. We evaluate and compare different input dimensionalities and two different CNN architectures. One of the architectures is a modified U-Net and the other a modified Mixed-Scale Dense Network (MS-D Net). Thus, we compare dilated convolutions for parallel multi-scale processing to the U-Net approach with traditional scaling operations based on the different input dimensionalities. Finally, we merge a set of 3D modified MS-D Nets and a set of 2D modified U-Nets as a stacked CNN-model to combine the different strengths of both model.