CTMQ: Cyclic Training of Convolutional Neural Networks with Multiple Quantization Steps

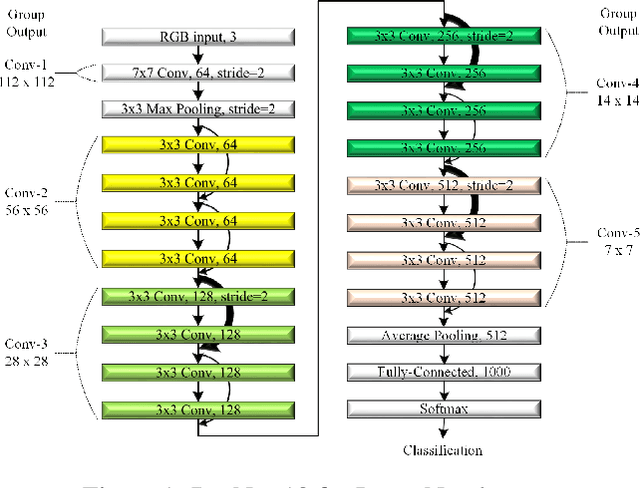
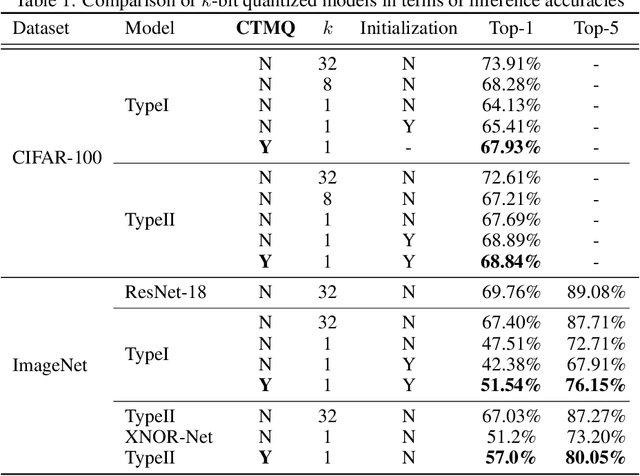
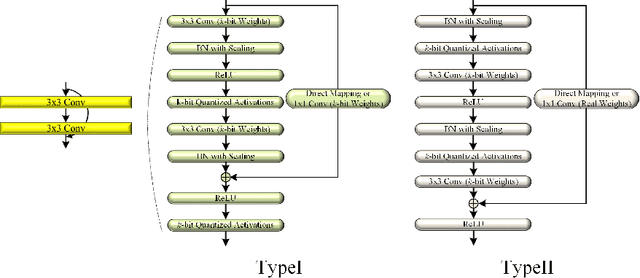
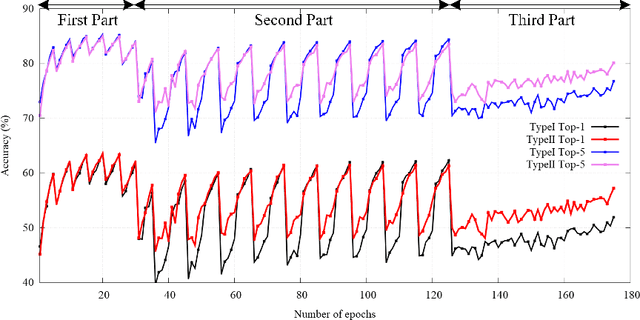
This paper proposes a training method having multiple cyclic training for achieving enhanced performance in low-bit quantized convolutional neural networks (CNNs). Quantization is a popular method for obtaining lightweight CNNs, where the initialization with a pretrained model is widely used to overcome degraded performance in low-resolution quantization. However, large quantization errors between real values and their low-bit quantized ones cause difficulties in achieving acceptable performance for complex networks and large datasets. The proposed training method softly delivers the knowledge of pretrained models to low-bit quantized models in multiple quantization steps. In each quantization step, the trained weights of a model are used to initialize the weights of the next model with the quantization bit depth reduced by one. With small change of the quantization bit depth, the performance gap can be bridged, thus providing better weight initialization. In cyclic training, after training a low-bit quantized model, its trained weights are used in the initialization of its accurate model to be trained. By using better training ability of the accurate model in an iterative manner, the proposed method can produce enhanced trained weights for the low-bit quantized model in each cycle. Notably, the training method can advance Top-1 and Top-5 accuracies of the binarized ResNet-18 on the ImageNet dataset by 5.80% and 6.85%, respectively.

PLAM: a Posit Logarithm-Approximate Multiplier for Power Efficient Posit-based DNNs

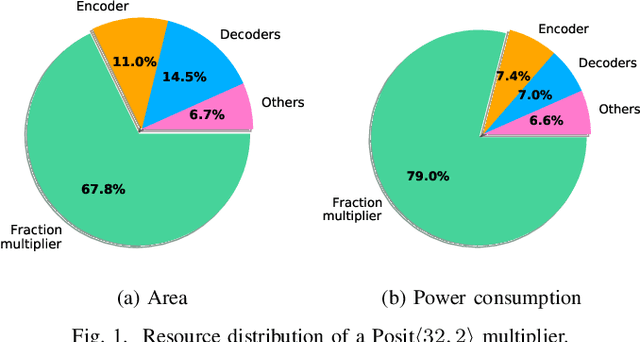
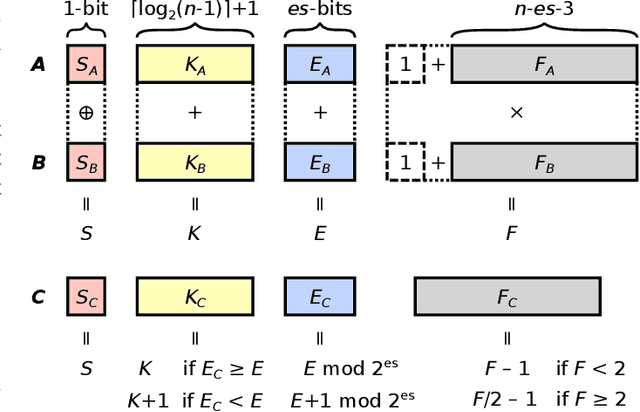
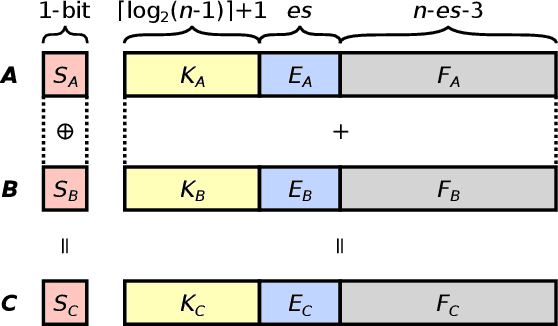
The Posit Number System was introduced in 2017 as a replacement for floating-point numbers. Since then, the community has explored its application in Neural Network related tasks and produced some unit designs which are still far from being competitive with their floating-point counterparts. This paper proposes a Posit Logarithm-Approximate Multiplication (PLAM) scheme to significantly reduce the complexity of posit multipliers, the most power-hungry units within Deep Neural Network architectures. When comparing with state-of-the-art posit multipliers, experiments show that the proposed technique reduces the area, power, and delay of hardware multipliers up to 72.86%, 81.79%, and 17.01%, respectively, without accuracy degradation.

Effects of Approximate Multiplication on Convolutional Neural Networks

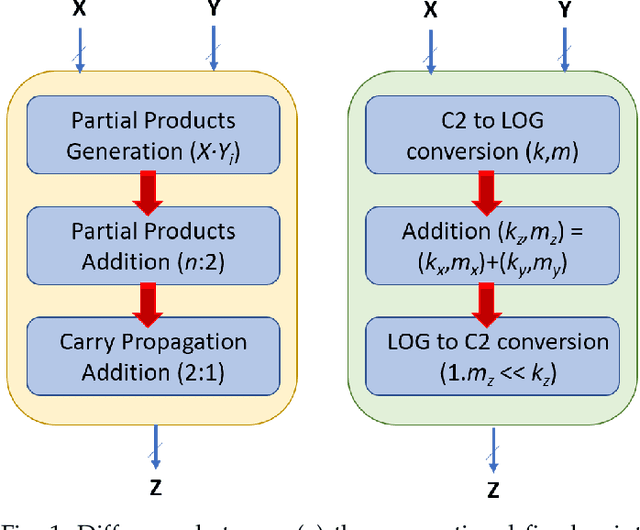
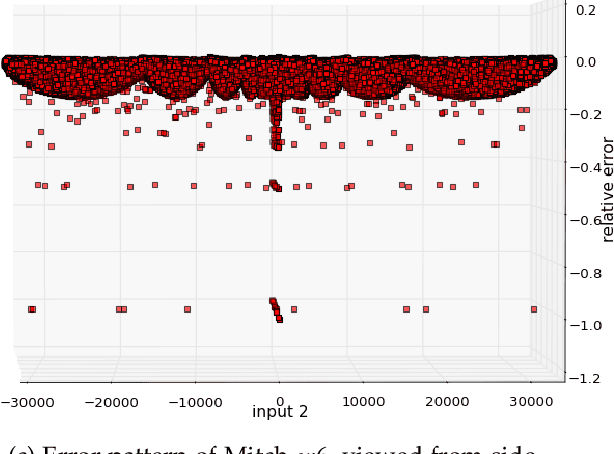
This paper analyzes the effects of approximate multiplication when performing inferences on deep convolutional neural networks (CNNs). The approximate multiplication can reduce the cost of underlying circuits so that CNN inferences can be performed more efficiently in hardware accelerators. The study identifies the critical factors in the convolution, fully-connected, and batch normalization layers that allow more accurate CNN predictions despite the errors from approximate multiplication. The same factors also provide an arithmetic explanation of why bfloat16 multiplication performs well on CNNs. The experiments are performed with recognized network architectures to show that the approximate multipliers can produce predictions that are nearly as accurate as the FP32 references, without additional training. For example, the ResNet and Inception-v4 models with Mitch-$w$6 multiplication produces Top-5 errors that are within 0.2% compared to the FP32 references. A brief cost comparison of Mitch-$w$6 against bfloat16 is presented, where a MAC operation saves up to 80% of energy compared to the bfloat16 arithmetic. The most far-reaching contribution of this paper is the analytical justification that multiplications can be approximated while additions need to be exact in CNN MAC operations.

Template-Based Posit Multiplication for Training and Inferring in Neural Networks

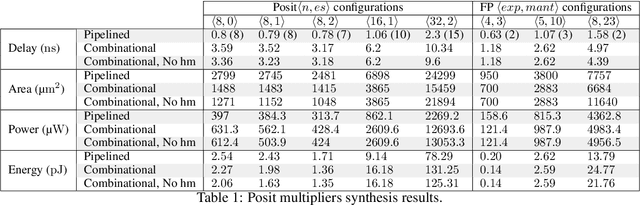
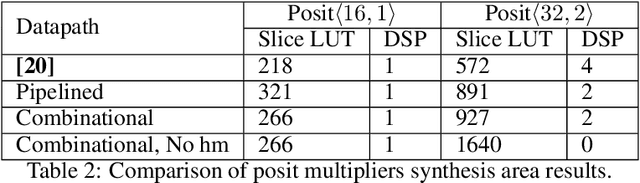
The posit number system is arguably the most promising and discussed topic in Arithmetic nowadays. The recent breakthroughs claimed by the format proposed by John L. Gustafson have put posits in the spotlight. In this work, we first describe an algorithm for multiplying two posit numbers, even when the number of exponent bits is zero. This configuration, scarcely tackled in literature, is particularly interesting because it allows the deployment of a fast sigmoid function. The proposed multiplication algorithm is then integrated as a template into the well-known FloPoCo framework. Synthesis results are shown to compare with the floating point multiplication offered by FloPoCo as well. Second, the performance of posits is studied in the scenario of Neural Networks in both training and inference stages. To the best of our knowledge, this is the first time that training is done with posit format, achieving promising results for a binary classification problem even with reduced posit configurations. In the inference stage, 8-bit posits are as good as floating point when dealing with the MNIST dataset, but lose some accuracy with CIFAR-10.