Raúl Murillo Montero
Template-Based Posit Multiplication for Training and Inferring in Neural Networks
Jul 09, 2019
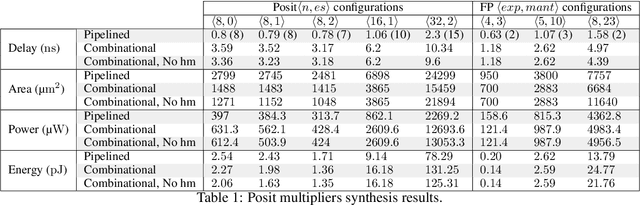

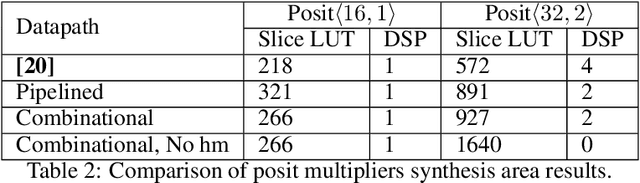
Abstract:The posit number system is arguably the most promising and discussed topic in Arithmetic nowadays. The recent breakthroughs claimed by the format proposed by John L. Gustafson have put posits in the spotlight. In this work, we first describe an algorithm for multiplying two posit numbers, even when the number of exponent bits is zero. This configuration, scarcely tackled in literature, is particularly interesting because it allows the deployment of a fast sigmoid function. The proposed multiplication algorithm is then integrated as a template into the well-known FloPoCo framework. Synthesis results are shown to compare with the floating point multiplication offered by FloPoCo as well. Second, the performance of posits is studied in the scenario of Neural Networks in both training and inference stages. To the best of our knowledge, this is the first time that training is done with posit format, achieving promising results for a binary classification problem even with reduced posit configurations. In the inference stage, 8-bit posits are as good as floating point when dealing with the MNIST dataset, but lose some accuracy with CIFAR-10.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge