A Review of Machine Learning-based Failure Management in Optical Networks

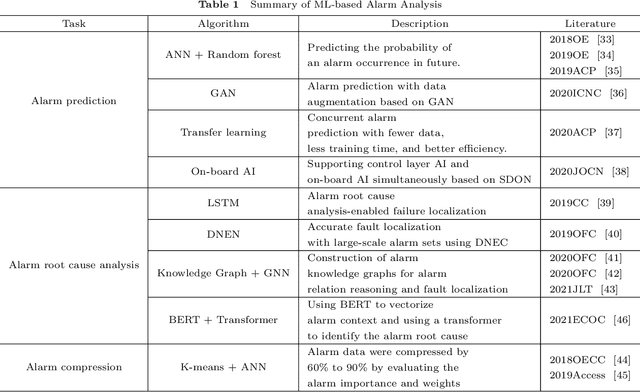
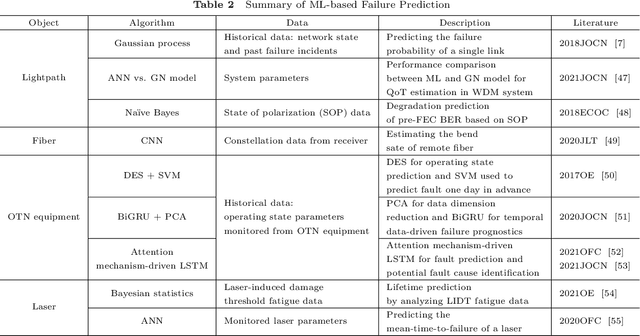
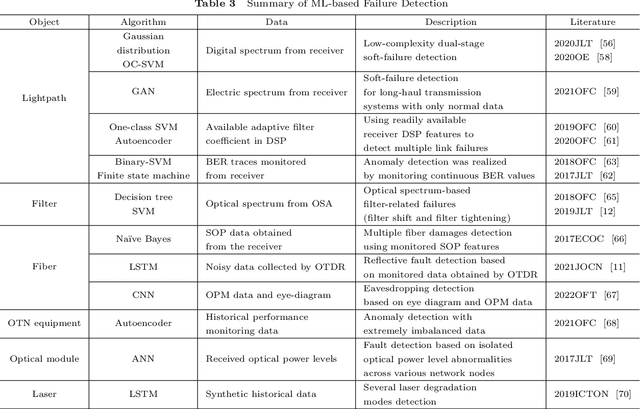
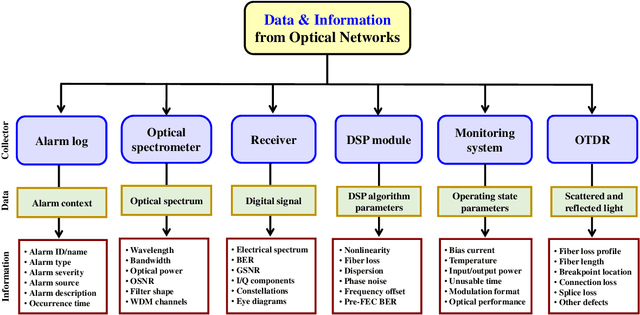
Failure management plays a significant role in optical networks. It ensures secure operation, mitigates potential risks, and executes proactive protection. Machine learning (ML) is considered to be an extremely powerful technique for performing comprehensive data analysis and complex network management and is widely utilized for failure management in optical networks to revolutionize the conventional manual methods. In this study, the background of failure management is introduced, where typical failure tasks, physical objects, ML algorithms, data source, and extracted information are illustrated in detail. An overview of the applications of ML in failure management is provided in terms of alarm analysis, failure prediction, failure detection, failure localization, and failure identification. Finally, the future directions on ML for failure management are discussed from the perspective of data, model, task, and emerging techniques.

Physics-informed Neural Network for Nonlinear Dynamics in Fiber Optics

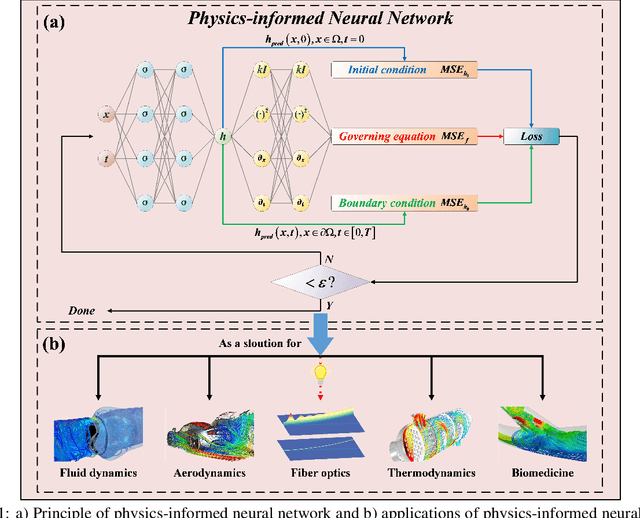
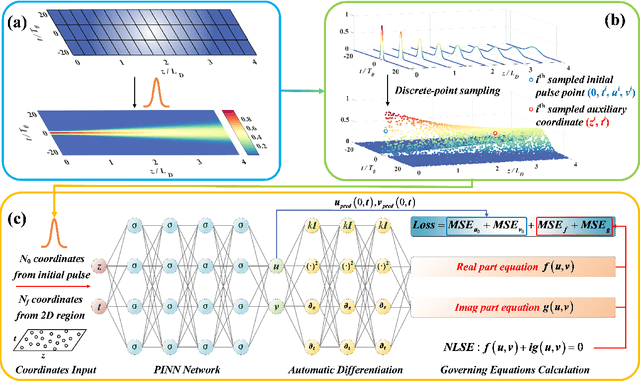
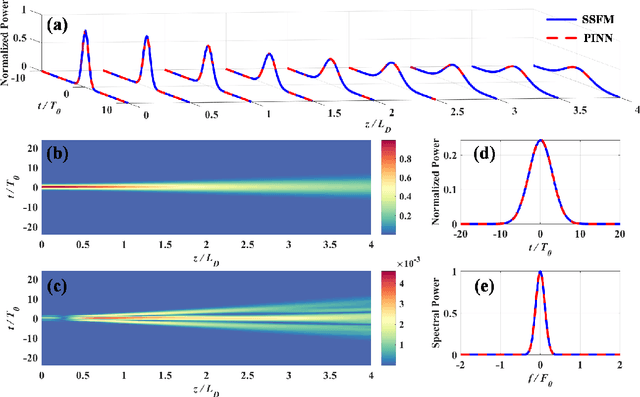
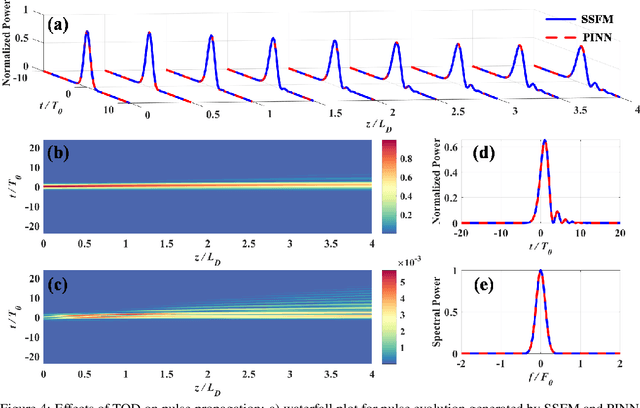
A physics-informed neural network (PINN) that combines deep learning with physics is studied to solve the nonlinear Schr\"odinger equation for learning nonlinear dynamics in fiber optics. We carry out a systematic investigation and comprehensive verification on PINN for multiple physical effects in optical fibers, including dispersion, self-phase modulation, and higher-order nonlinear effects. Moreover, both special case (soliton propagation) and general case (multi-pulse propagation) are investigated and realized with PINN. In the previous studies, the PINN was mainly effective for single scenario. To overcome this problem, the physical parameters (pulse peak power and amplitudes of sub-pulses) are hereby embedded as additional input parameter controllers, which allow PINN to learn the physical constraints of different scenarios and perform good generalizability. Furthermore, PINN exhibits better performance than the data-driven neural network using much less data, and its computational complexity (in terms of number of multiplications) is much lower than that of the split-step Fourier method. The results report here show that the PINN is not only an effective partial differential equation solver, but also a prospective technique to advance the scientific computing and automatic modeling in fiber optics.