A Ray Intersection Algorithm for Fast Growth Distance Computation Between Convex Sets

In this paper, we discuss an efficient algorithm for computing the growth distance between two compact convex sets with representable support functions. The growth distance between two sets is the minimum scaling factor such that the sets intersect when scaled about some center points. Unlike the minimum distance between sets, the growth distance provides a unified measure for set intersection and separation. We first reduce the growth distance problem to an equivalent ray intersection problem on the Minkowski difference set. Then, we propose an algorithm to solve the ray intersection problem by iteratively constructing inner and outer polyhedral approximations of the Minkowski difference set. We show that our algorithm satisfies several key properties, such as primal and dual feasibility and monotone convergence. We provide extensive benchmark results for our algorithm and show that our open-source implementation achieves state-of-the-art performance across a wide variety of convex sets. Finally, we demonstrate robotics applications of our algorithm in motion planning and rigid-body simulation.

Nonsmooth Control Barrier Functions for Obstacle Avoidance between Convex Regions

In this paper, we focus on non-conservative obstacle avoidance between robots with control affine dynamics with strictly convex and polytopic shapes. The core challenge for this obstacle avoidance problem is that the minimum distance between strictly convex regions or polytopes is generally implicit and non-smooth, such that distance constraints cannot be enforced directly in the optimization problem. To handle this challenge, we employ non-smooth control barrier functions to reformulate the avoidance problem in the dual space, with the positivity of the minimum distance between robots equivalently expressed using a quadratic program. Our approach is proven to guarantee system safety. We theoretically analyze the smoothness properties of the minimum distance quadratic program and its KKT conditions. We validate our approach by demonstrating computationally-efficient obstacle avoidance for multi-agent robotic systems with strictly convex and polytopic shapes. To our best knowledge, this is the first time a real-time QP problem can be formulated for general non-conservative avoidance between strictly convex shapes and polytopes.

Walking in Narrow Spaces: Safety-critical Locomotion Control for Quadrupedal Robots with Duality-based Optimization

This paper presents a safety-critical locomotion control framework for quadrupedal robots. Our goal is to enable quadrupedal robots to safely navigate in cluttered environments. To tackle this, we introduce exponential Discrete Control Barrier Functions (exponential DCBFs) with duality-based obstacle avoidance constraints into a Nonlinear Model Predictive Control (NMPC) with Whole-Body Control (WBC) framework for quadrupedal locomotion control. This enables us to use polytopes to describe the shapes of the robot and obstacles for collision avoidance while doing locomotion control of quadrupedal robots. Compared to most prior work, especially using CBFs, that utilize spherical and conservative approximation for obstacle avoidance, this work demonstrates a quadrupedal robot autonomously and safely navigating through very tight spaces in the real world. (Our open-source code is available at github.com/HybridRobotics/quadruped_nmpc_dcbf_duality, and the video is available at youtu.be/p1gSQjwXm1Q.)

Bridging Model-based Safety and Model-free Reinforcement Learning through System Identification of Low Dimensional Linear Models

Bridging model-based safety and model-free reinforcement learning (RL) for dynamic robots is appealing since model-based methods are able to provide formal safety guarantees, while RL-based methods are able to exploit the robot agility by learning from the full-order system dynamics. However, current approaches to tackle this problem are mostly restricted to simple systems. In this paper, we propose a new method to combine model-based safety with model-free reinforcement learning by explicitly finding a low-dimensional model of the system controlled by a RL policy and applying stability and safety guarantees on that simple model. We use a complex bipedal robot Cassie, which is a high dimensional nonlinear system with hybrid dynamics and underactuation, and its RL-based walking controller as an example. We show that a low-dimensional dynamical model is sufficient to capture the dynamics of the closed-loop system. We demonstrate that this model is linear, asymptotically stable, and is decoupled across control input in all dimensions. We further exemplify that such linearity exists even when using different RL control policies. Such results point out an interesting direction to understand the relationship between RL and optimal control: whether RL tends to linearize the nonlinear system during training in some cases. Furthermore, we illustrate that the found linear model is able to provide guarantees by safety-critical optimal control framework, e.g., Model Predictive Control with Control Barrier Functions, on an example of autonomous navigation using Cassie while taking advantage of the agility provided by the RL-based controller.

A Fast Computational Optimization for Control and Trajectory Planning for Obstacle Avoidance between Polytopes

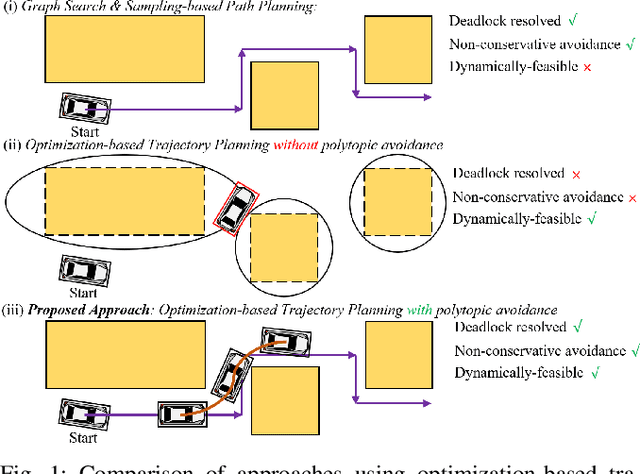
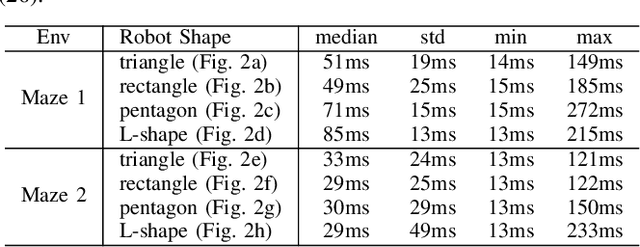
Obstacle avoidance between polytopes is a challenging topic for optimal control and optimization-based trajectory planning problems. Existing work either solves this problem through mixed-integer optimization, relying on simplification of system dynamics, or through model predictive control with dual variables using distance constraints, requiring long horizons for obstacle avoidance. In either case, the solution can only be applied as an offline planning algorithm. In this paper, we exploit the property that a smaller horizon is sufficient for obstacle avoidance by using discrete-time control barrier function (DCBF) constraints and we propose a novel optimization formulation with dual variables based on DCBFs to generate a collision-free dynamically-feasible trajectory. The proposed optimization formulation has lower computational complexity compared to existing work and can be used as a fast online algorithm for control and planning for general nonlinear dynamical systems. We validate our algorithm on different robot shapes using numerical simulations with a kinematic bicycle model, resulting in successful navigation through maze environments with polytopic obstacles.

A Duality-based Approach for Real-time Obstacle Avoidance between Polytopes with Control Barrier Functions

Developing controllers for obstacle avoidance between polytopes is a challenging and necessary problem for navigation in a tight space. Traditional approaches can only formulate the obstacle avoidance problem as an offline optimization problem. To address these challenges, we propose a duality-based safety-critical optimal control using control barrier functions for obstacle avoidance between polytopes, which can be solved in real-time with a QP-based optimization problem. A dual optimization problem is introduced to represent the minimum distance between polytopes and the Lagrangian function for the dual form is applied to construct a control barrier function. We demonstrate the proposed controller on a moving sofa problem where non-conservative maneuvers can be achieved in a tight space.