Kernel Dependence Regularizers and Gaussian Processes with Applications to Algorithmic Fairness

Current adoption of machine learning in industrial, societal and economical activities has raised concerns about the fairness, equity and ethics of automated decisions. Predictive models are often developed using biased datasets and thus retain or even exacerbate biases in their decisions and recommendations. Removing the sensitive covariates, such as gender or race, is insufficient to remedy this issue since the biases may be retained due to other related covariates. We present a regularization approach to this problem that trades off predictive accuracy of the learned models (with respect to biased labels) for the fairness in terms of statistical parity, i.e. independence of the decisions from the sensitive covariates. In particular, we consider a general framework of regularized empirical risk minimization over reproducing kernel Hilbert spaces and impose an additional regularizer of dependence between predictors and sensitive covariates using kernel-based measures of dependence, namely the Hilbert-Schmidt Independence Criterion (HSIC) and its normalized version. This approach leads to a closed-form solution in the case of squared loss, i.e. ridge regression. Moreover, we show that the dependence regularizer has an interpretation as modifying the corresponding Gaussian process (GP) prior. As a consequence, a GP model with a prior that encourages fairness to sensitive variables can be derived, allowing principled hyperparameter selection and studying of the relative relevance of covariates under fairness constraints. Experimental results in synthetic examples and in real problems of income and crime prediction illustrate the potential of the approach to improve fairness of automated decisions.

Remote Sensing Image Classification with Large Scale Gaussian Processes

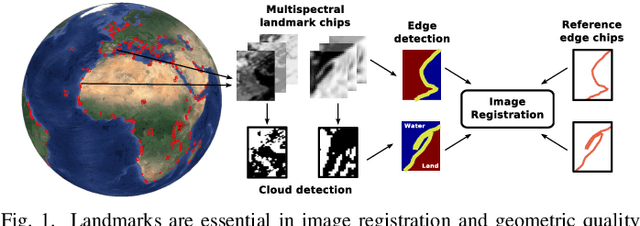
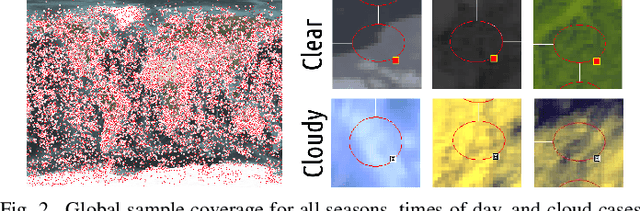
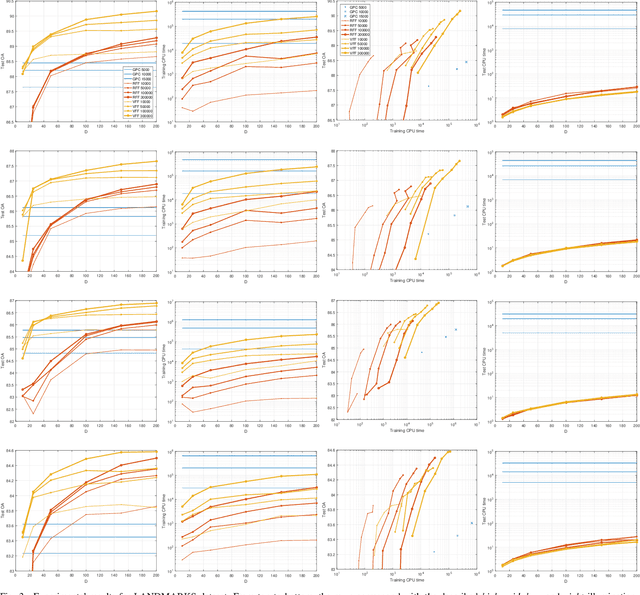
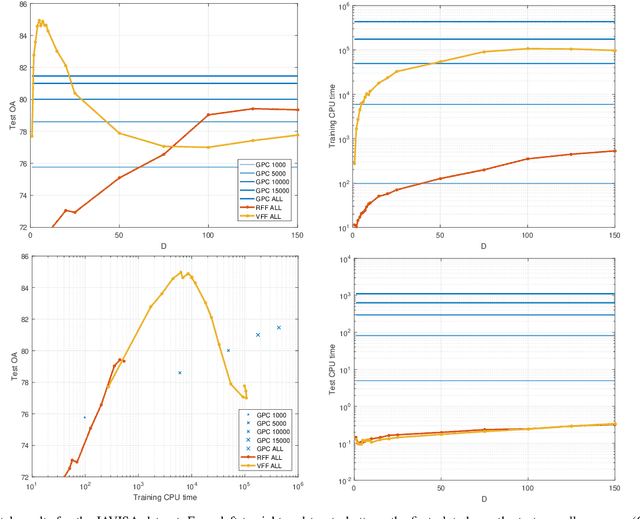
Current remote sensing image classification problems have to deal with an unprecedented amount of heterogeneous and complex data sources. Upcoming missions will soon provide large data streams that will make land cover/use classification difficult. Machine learning classifiers can help at this, and many methods are currently available. A popular kernel classifier is the Gaussian process classifier (GPC), since it approaches the classification problem with a solid probabilistic treatment, thus yielding confidence intervals for the predictions as well as very competitive results to state-of-the-art neural networks and support vector machines. However, its computational cost is prohibitive for large scale applications, and constitutes the main obstacle precluding wide adoption. This paper tackles this problem by introducing two novel efficient methodologies for Gaussian Process (GP) classification. We first include the standard random Fourier features approximation into GPC, which largely decreases its computational cost and permits large scale remote sensing image classification. In addition, we propose a model which avoids randomly sampling a number of Fourier frequencies, and alternatively learns the optimal ones within a variational Bayes approach. The performance of the proposed methods is illustrated in complex problems of cloud detection from multispectral imagery and infrared sounding data. Excellent empirical results support the proposal in both computational cost and accuracy.