Aditya Nugraha
RIKEN AIP
Generalized Fast Multichannel Nonnegative Matrix Factorization Based on Gaussian Scale Mixtures for Blind Source Separation
May 11, 2022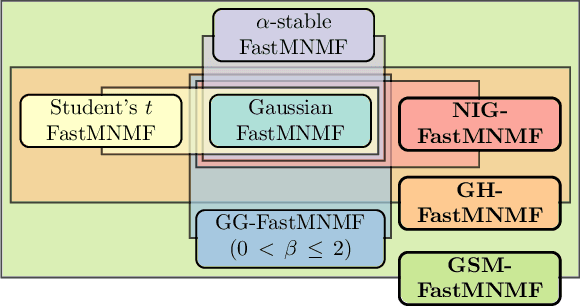
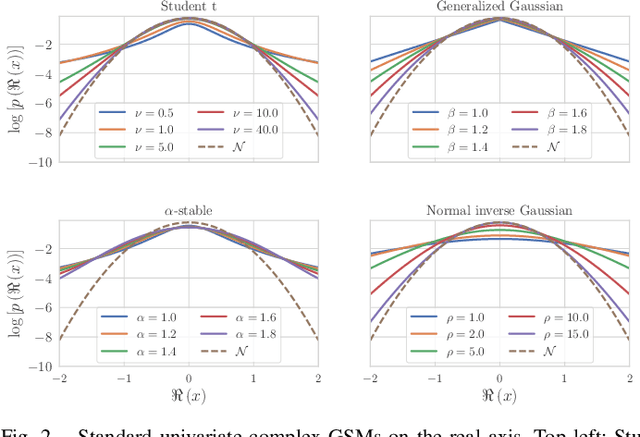
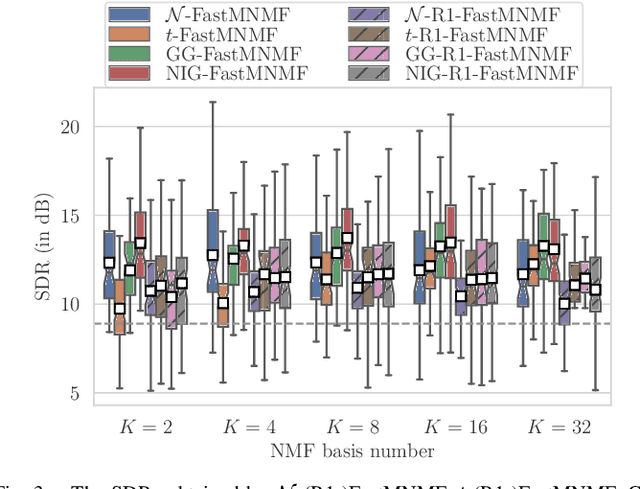
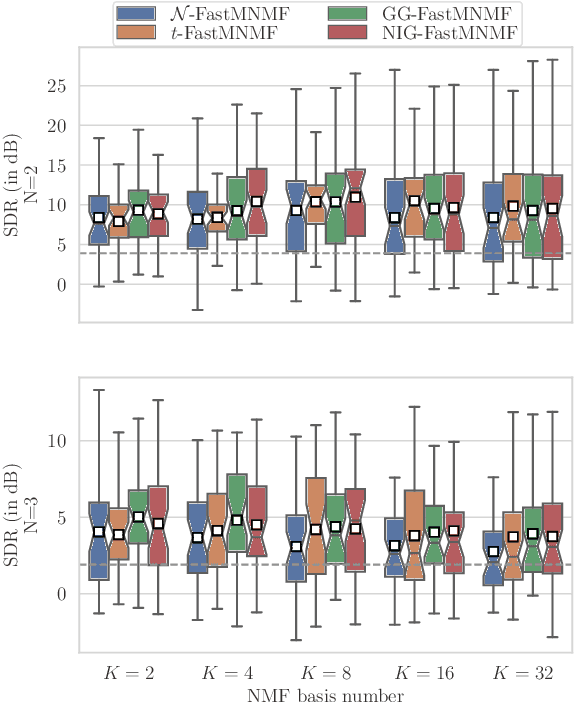
Abstract:This paper describes heavy-tailed extensions of a state-of-the-art versatile blind source separation method called fast multichannel nonnegative matrix factorization (FastMNMF) from a unified point of view. The common way of deriving such an extension is to replace the multivariate complex Gaussian distribution in the likelihood function with its heavy-tailed generalization, e.g., the multivariate complex Student's t and leptokurtic generalized Gaussian distributions, and tailor-make the corresponding parameter optimization algorithm. Using a wider class of heavy-tailed distributions called a Gaussian scale mixture (GSM), i.e., a mixture of Gaussian distributions whose variances are perturbed by positive random scalars called impulse variables, we propose GSM-FastMNMF and develop an expectationmaximization algorithm that works even when the probability density function of the impulse variables have no analytical expressions. We show that existing heavy-tailed FastMNMF extensions are instances of GSM-FastMNMF and derive a new instance based on the generalized hyperbolic distribution that include the normal-inverse Gaussian, Student's t, and Gaussian distributions as the special cases. Our experiments show that the normalinverse Gaussian FastMNMF outperforms the state-of-the-art FastMNMF extensions and ILRMA model in speech enhancement and separation in terms of the signal-to-distortion ratio.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge