ViT-NeBLa: A Hybrid Vision Transformer and Neural Beer-Lambert Framework for Single-View 3D Reconstruction of Oral Anatomy from Panoramic Radiographs

Dental diagnosis relies on two primary imaging modalities: panoramic radiographs (PX) providing 2D oral cavity representations, and Cone-Beam Computed Tomography (CBCT) offering detailed 3D anatomical information. While PX images are cost-effective and accessible, their lack of depth information limits diagnostic accuracy. CBCT addresses this but presents drawbacks including higher costs, increased radiation exposure, and limited accessibility. Existing reconstruction models further complicate the process by requiring CBCT flattening or prior dental arch information, often unavailable clinically. We introduce ViT-NeBLa, a vision transformer-based Neural Beer-Lambert model enabling accurate 3D reconstruction directly from single PX. Our key innovations include: (1) enhancing the NeBLa framework with Vision Transformers for improved reconstruction capabilities without requiring CBCT flattening or prior dental arch information, (2) implementing a novel horseshoe-shaped point sampling strategy with non-intersecting rays that eliminates intermediate density aggregation required by existing models due to intersecting rays, reducing sampling point computations by $52 \%$, (3) replacing CNN-based U-Net with a hybrid ViT-CNN architecture for superior global and local feature extraction, and (4) implementing learnable hash positional encoding for better higher-dimensional representation of 3D sample points compared to existing Fourier-based dense positional encoding. Experiments demonstrate that ViT-NeBLa significantly outperforms prior state-of-the-art methods both quantitatively and qualitatively, offering a cost-effective, radiation-efficient alternative for enhanced dental diagnostics.

Physics Informed Kolmogorov-Arnold Neural Networks for Dynamical Analysis via Efficent-KAN and WAV-KAN

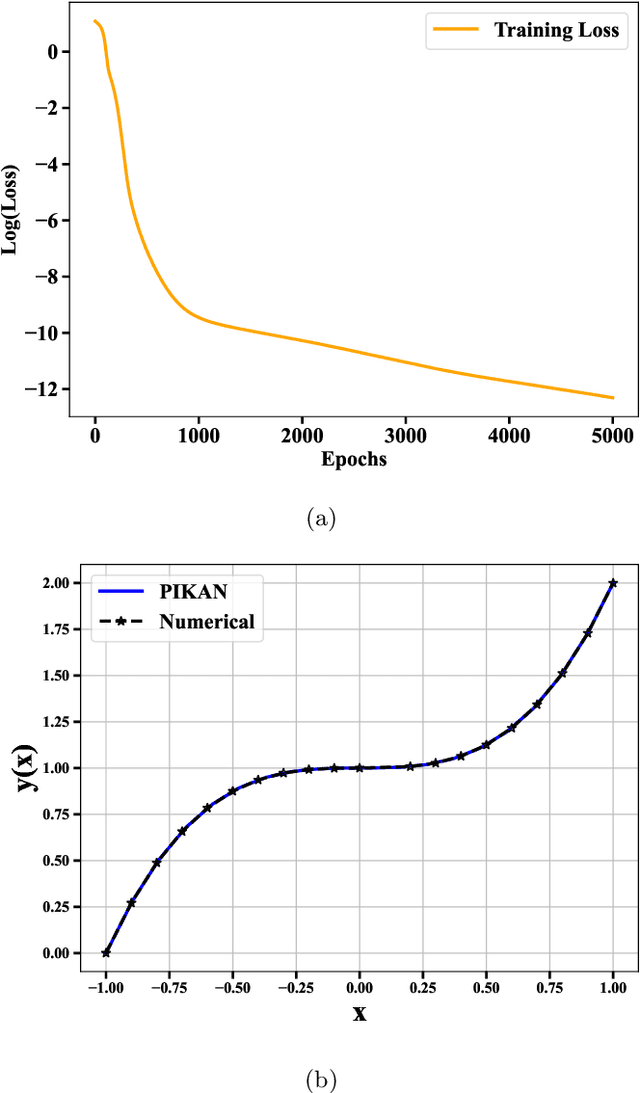
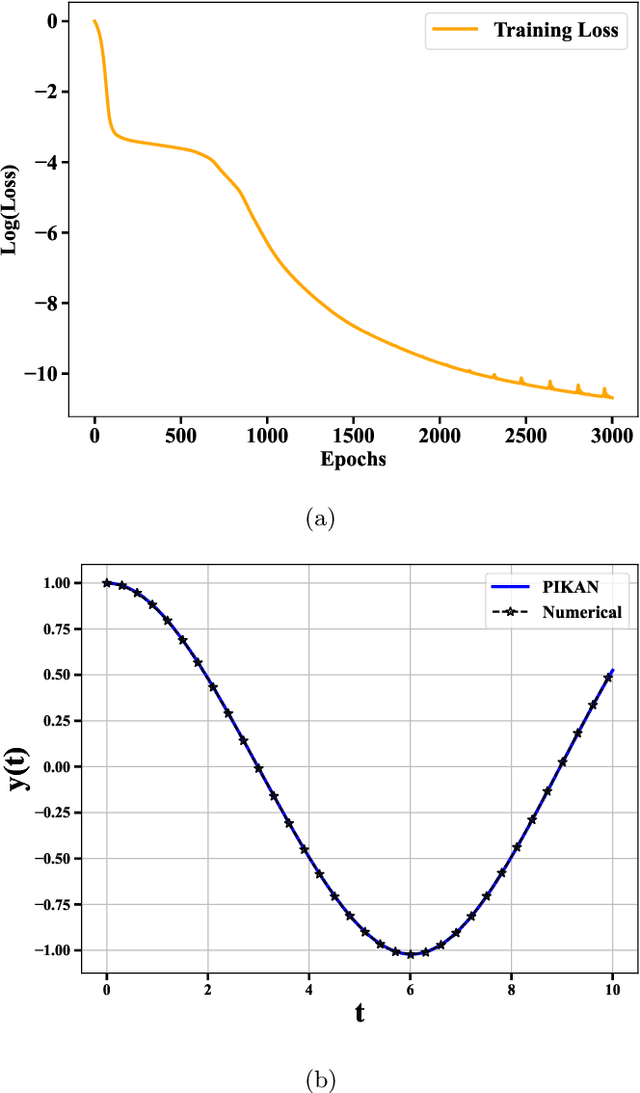
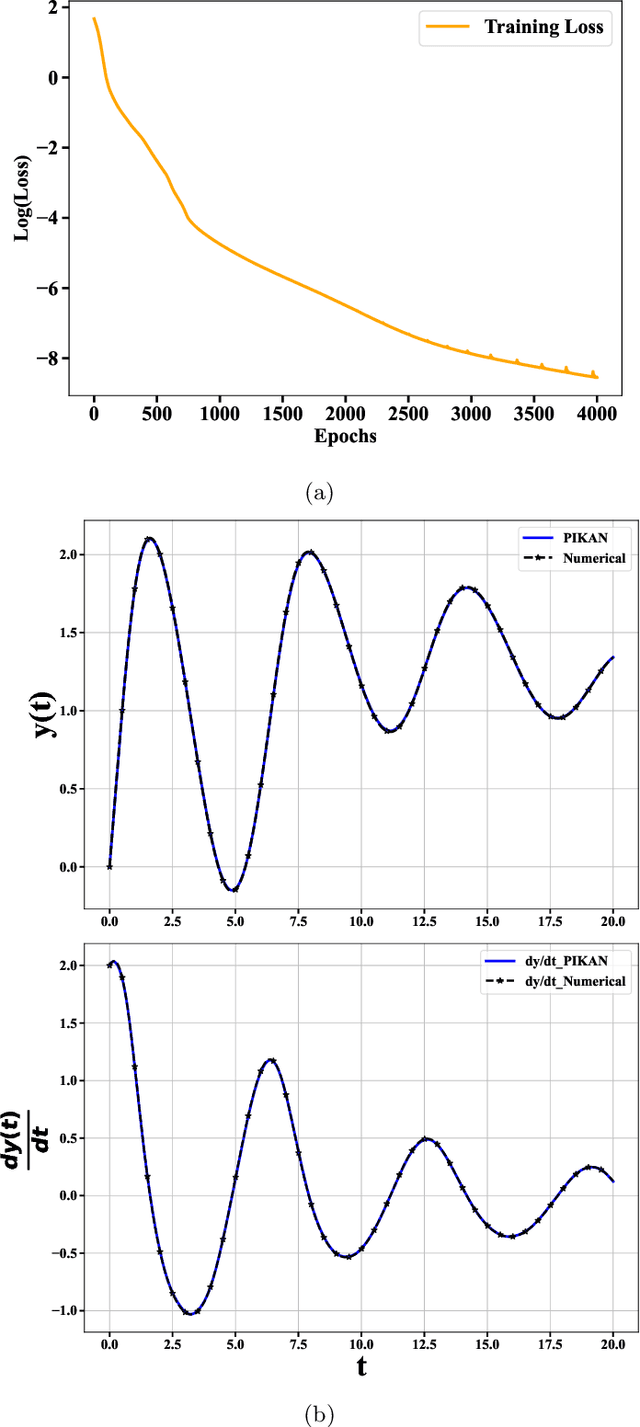
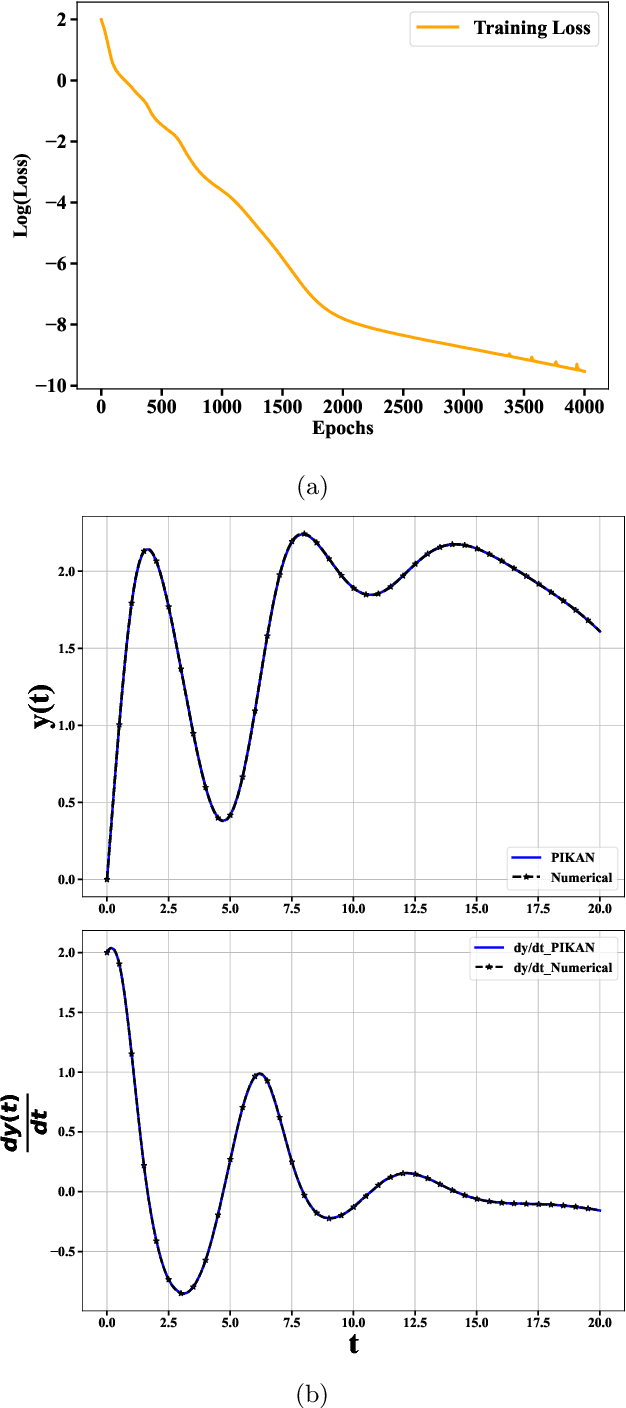
Physics-informed neural networks have proven to be a powerful tool for solving differential equations, leveraging the principles of physics to inform the learning process. However, traditional deep neural networks often face challenges in achieving high accuracy without incurring significant computational costs. In this work, we implement the Physics-Informed Kolmogorov-Arnold Neural Networks (PIKAN) through efficient-KAN and WAV-KAN, which utilize the Kolmogorov-Arnold representation theorem. PIKAN demonstrates superior performance compared to conventional deep neural networks, achieving the same level of accuracy with fewer layers and reduced computational overhead. We explore both B-spline and wavelet-based implementations of PIKAN and benchmark their performance across various ordinary and partial differential equations using unsupervised (data-free) and supervised (data-driven) techniques. For certain differential equations, the data-free approach suffices to find accurate solutions, while in more complex scenarios, the data-driven method enhances the PIKAN's ability to converge to the correct solution. We validate our results against numerical solutions and achieve $99 \%$ accuracy in most scenarios.

AI-Dentify: Deep learning for proximal caries detection on bitewing x-ray -- HUNT4 Oral Health Study

Background: Dental caries diagnosis requires the manual inspection of diagnostic bitewing images of the patient, followed by a visual inspection and probing of the identified dental pieces with potential lesions. Yet the use of artificial intelligence, and in particular deep-learning, has the potential to aid in the diagnosis by providing a quick and informative analysis of the bitewing images. Methods: A dataset of 13,887 bitewings from the HUNT4 Oral Health Study were annotated individually by six different experts, and used to train three different object detection deep-learning architectures: RetinaNet (ResNet50), YOLOv5 (M size), and EfficientDet (D0 and D1 sizes). A consensus dataset of 197 images, annotated jointly by the same six dentist, was used for evaluation. A five-fold cross validation scheme was used to evaluate the performance of the AI models. Results: the trained models show an increase in average precision and F1-score, and decrease of false negative rate, with respect to the dental clinicians. Out of the three architectures studied, YOLOv5 shows the largest improvement, reporting 0.647 mean average precision, 0.548 mean F1-score, and 0.149 mean false negative rate. Whereas the best annotators on each of these metrics reported 0.299, 0.495, and 0.164 respectively. Conclusion: Deep-learning models have shown the potential to assist dental professionals in the diagnosis of caries. Yet, the task remains challenging due to the artifacts natural to the bitewings.

A KdV-like advection-dispersion equation with some remarkable properties

We discuss a new non-linear PDE, u_t + (2 u_xx/u) u_x = epsilon u_xxx, invariant under scaling of dependent variable and referred to here as SIdV. It is one of the simplest such translation and space-time reflection-symmetric first order advection-dispersion equations. This PDE (with dispersion coefficient unity) was discovered in a genetic programming search for equations sharing the KdV solitary wave solution. It provides a bridge between non-linear advection, diffusion and dispersion. Special cases include the mKdV and linear dispersive equations. We identify two conservation laws, though initial investigations indicate that SIdV does not follow from a polynomial Lagrangian of the KdV sort. Nevertheless, it possesses solitary and periodic travelling waves. Moreover, numerical simulations reveal recurrence properties usually associated with integrable systems. KdV and SIdV are the simplest in an infinite dimensional family of equations sharing the KdV solitary wave. SIdV and its generalizations may serve as a testing ground for numerical and analytical techniques and be a rich source for further explorations.