Subhajit Patra
From Classical to Quantum Reinforcement Learning and Its Applications in Quantum Control: A Beginner's Tutorial
Jan 13, 2026Abstract:This tutorial is designed to make reinforcement learning (RL) more accessible to undergraduate students by offering clear, example-driven explanations. It focuses on bridging the gap between RL theory and practical coding applications, addressing common challenges that students face when transitioning from conceptual understanding to implementation. Through hands-on examples and approachable explanations, the tutorial aims to equip students with the foundational skills needed to confidently apply RL techniques in real-world scenarios.
Physics Informed Kolmogorov-Arnold Neural Networks for Dynamical Analysis via Efficent-KAN and WAV-KAN
Jul 29, 2024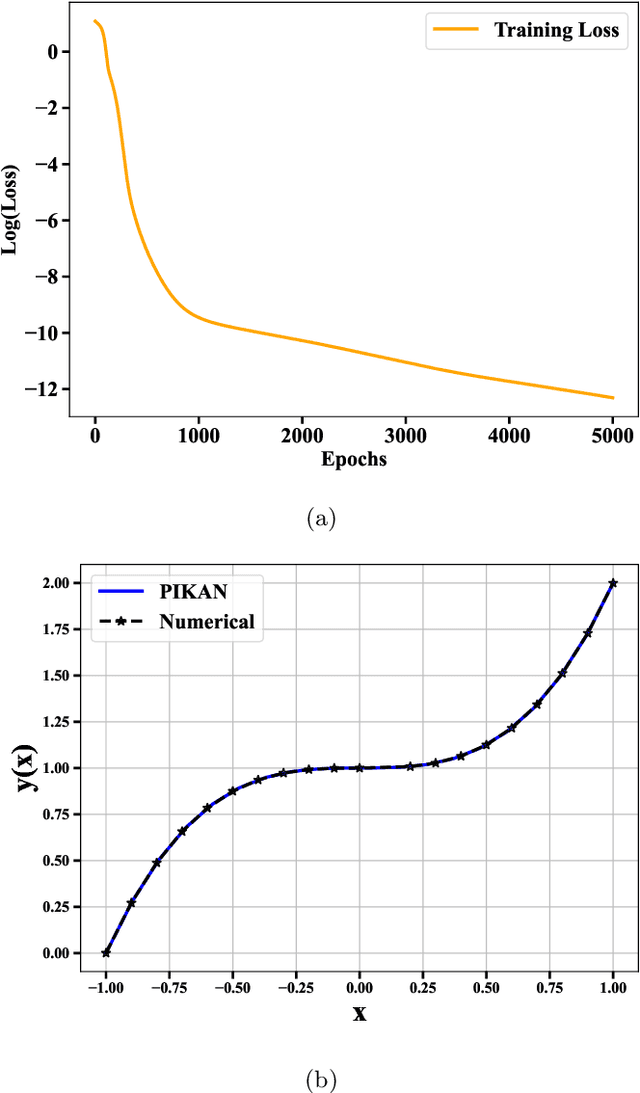
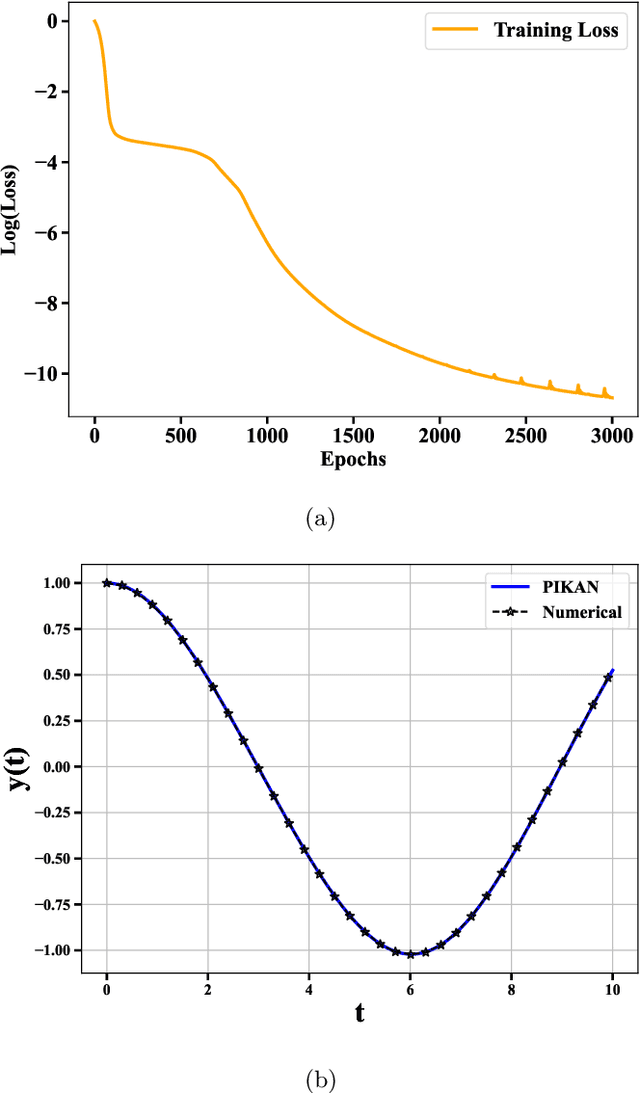
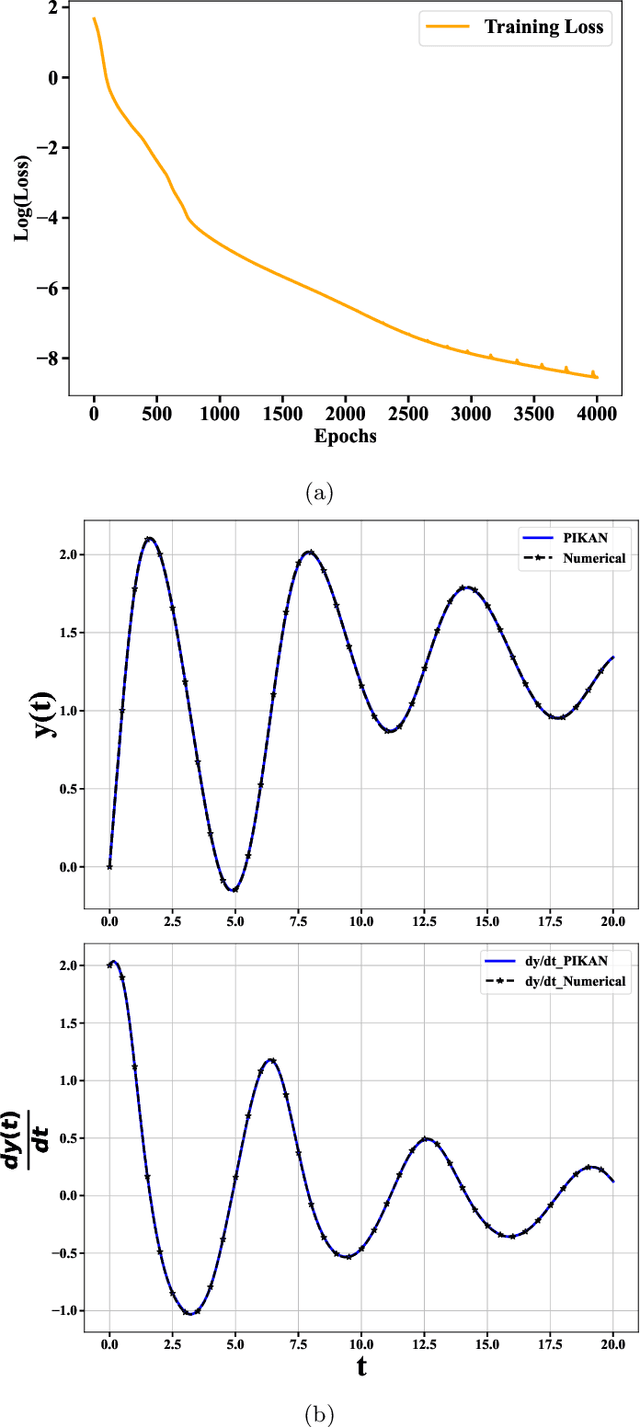
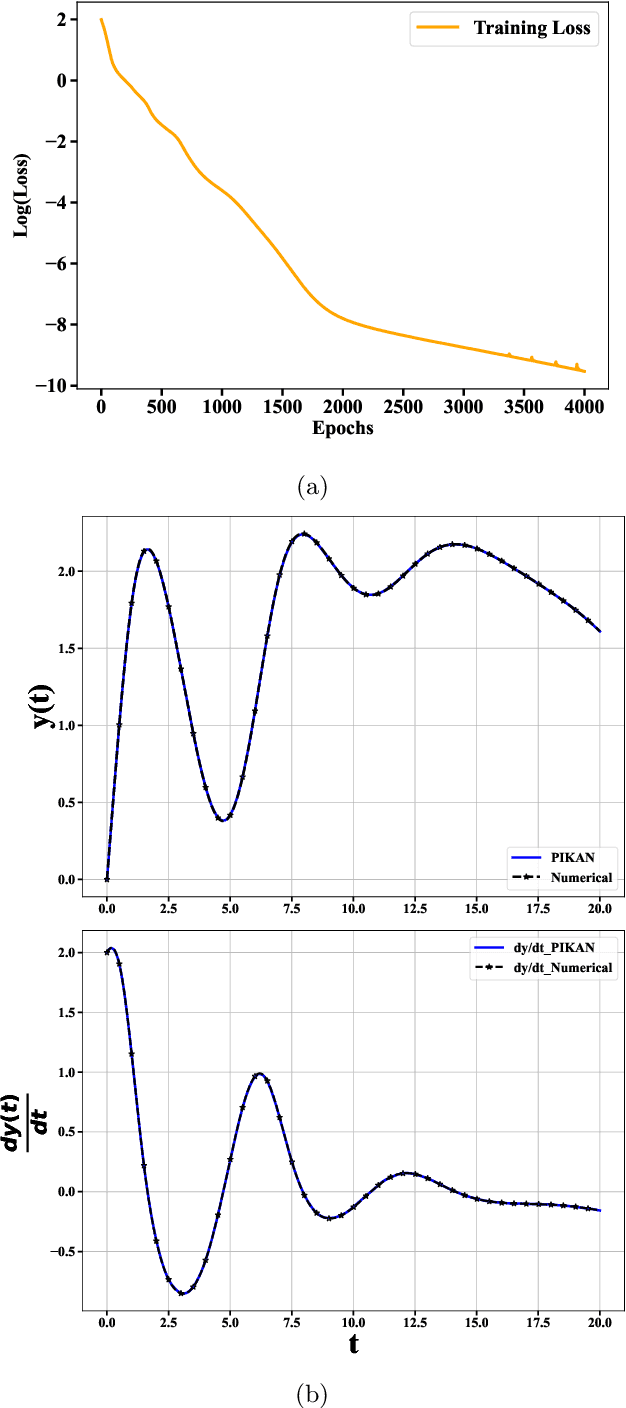
Abstract:Physics-informed neural networks have proven to be a powerful tool for solving differential equations, leveraging the principles of physics to inform the learning process. However, traditional deep neural networks often face challenges in achieving high accuracy without incurring significant computational costs. In this work, we implement the Physics-Informed Kolmogorov-Arnold Neural Networks (PIKAN) through efficient-KAN and WAV-KAN, which utilize the Kolmogorov-Arnold representation theorem. PIKAN demonstrates superior performance compared to conventional deep neural networks, achieving the same level of accuracy with fewer layers and reduced computational overhead. We explore both B-spline and wavelet-based implementations of PIKAN and benchmark their performance across various ordinary and partial differential equations using unsupervised (data-free) and supervised (data-driven) techniques. For certain differential equations, the data-free approach suffices to find accurate solutions, while in more complex scenarios, the data-driven method enhances the PIKAN's ability to converge to the correct solution. We validate our results against numerical solutions and achieve $99 \%$ accuracy in most scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge