ViT-NeBLa: A Hybrid Vision Transformer and Neural Beer-Lambert Framework for Single-View 3D Reconstruction of Oral Anatomy from Panoramic Radiographs

Dental diagnosis relies on two primary imaging modalities: panoramic radiographs (PX) providing 2D oral cavity representations, and Cone-Beam Computed Tomography (CBCT) offering detailed 3D anatomical information. While PX images are cost-effective and accessible, their lack of depth information limits diagnostic accuracy. CBCT addresses this but presents drawbacks including higher costs, increased radiation exposure, and limited accessibility. Existing reconstruction models further complicate the process by requiring CBCT flattening or prior dental arch information, often unavailable clinically. We introduce ViT-NeBLa, a vision transformer-based Neural Beer-Lambert model enabling accurate 3D reconstruction directly from single PX. Our key innovations include: (1) enhancing the NeBLa framework with Vision Transformers for improved reconstruction capabilities without requiring CBCT flattening or prior dental arch information, (2) implementing a novel horseshoe-shaped point sampling strategy with non-intersecting rays that eliminates intermediate density aggregation required by existing models due to intersecting rays, reducing sampling point computations by $52 \%$, (3) replacing CNN-based U-Net with a hybrid ViT-CNN architecture for superior global and local feature extraction, and (4) implementing learnable hash positional encoding for better higher-dimensional representation of 3D sample points compared to existing Fourier-based dense positional encoding. Experiments demonstrate that ViT-NeBLa significantly outperforms prior state-of-the-art methods both quantitatively and qualitatively, offering a cost-effective, radiation-efficient alternative for enhanced dental diagnostics.

Panorama Tomosynthesis from Head CBCT with Simulated Projection Geometry

Cone Beam Computed Tomography (CBCT) and Panoramic X-rays are the most commonly used imaging modalities in dental health care. CBCT can produce three-dimensional views of a patient's head, providing clinicians with better diagnostic capability, whereas Panoramic X-ray can capture the entire maxillofacial region in a single image. If the CBCT is already available, it can be beneficial to synthesize a Panoramic X-ray, thereby avoiding an immediate additional scan and extra radiation exposure. Existing methods focus on delineating an approximate dental arch and creating orthogonal projections along this arch. However, no golden standard is available for such dental arch extractions, and this choice can affect the quality of synthesized X-rays. To avoid such issues, we propose a novel method for synthesizing Panoramic X-rays from diverse head CBCTs, employing a simulated projection geometry and dynamic rotation centers. Our method effectively synthesized panoramic views from CBCT, even for patients with missing or nonexistent teeth and in the presence of severe metal implants. Our results demonstrate that this method can generate high-quality panoramic images irrespective of the CBCT scanner geometry.

Physics Informed Kolmogorov-Arnold Neural Networks for Dynamical Analysis via Efficent-KAN and WAV-KAN

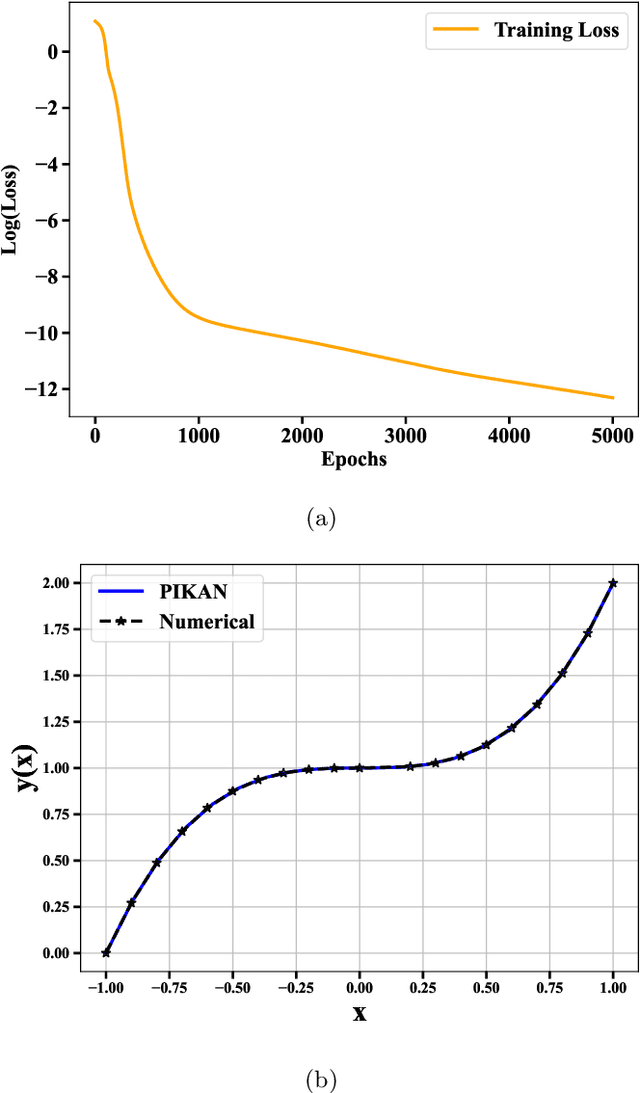
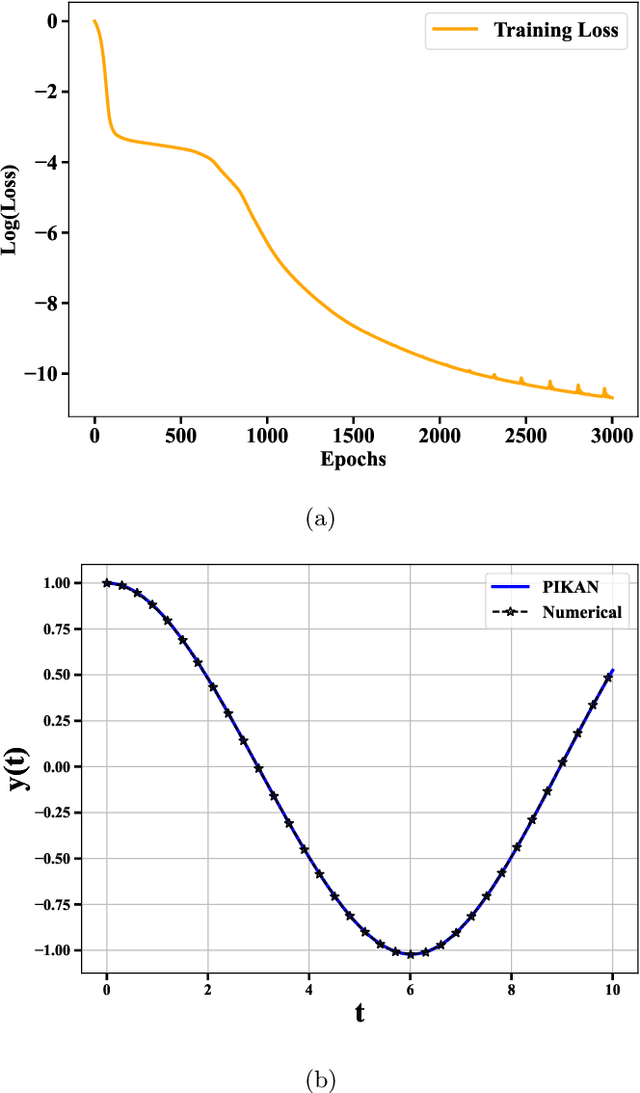
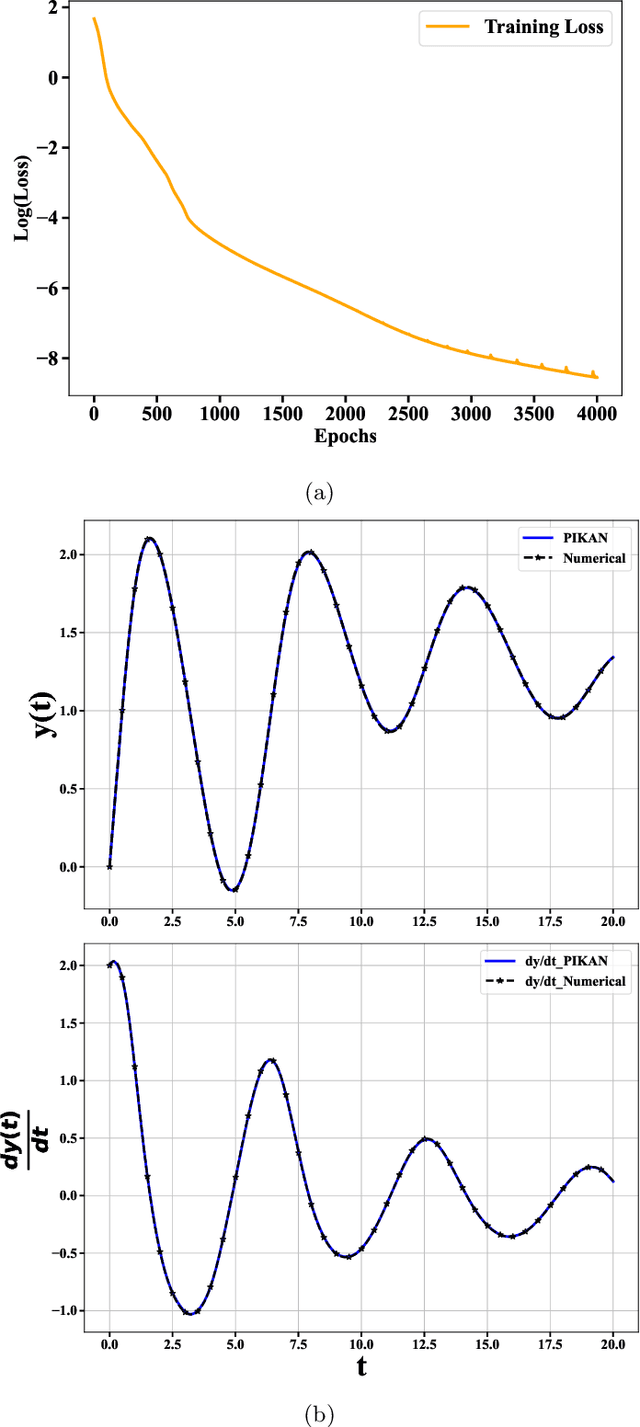
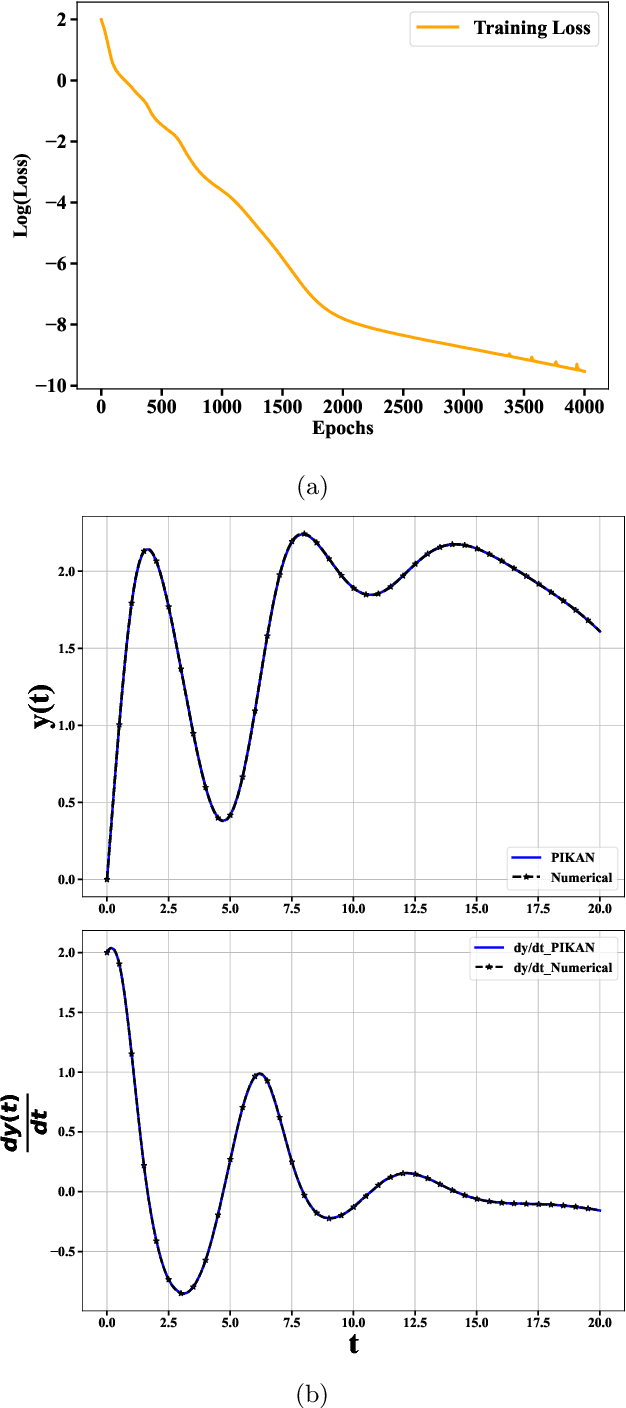
Physics-informed neural networks have proven to be a powerful tool for solving differential equations, leveraging the principles of physics to inform the learning process. However, traditional deep neural networks often face challenges in achieving high accuracy without incurring significant computational costs. In this work, we implement the Physics-Informed Kolmogorov-Arnold Neural Networks (PIKAN) through efficient-KAN and WAV-KAN, which utilize the Kolmogorov-Arnold representation theorem. PIKAN demonstrates superior performance compared to conventional deep neural networks, achieving the same level of accuracy with fewer layers and reduced computational overhead. We explore both B-spline and wavelet-based implementations of PIKAN and benchmark their performance across various ordinary and partial differential equations using unsupervised (data-free) and supervised (data-driven) techniques. For certain differential equations, the data-free approach suffices to find accurate solutions, while in more complex scenarios, the data-driven method enhances the PIKAN's ability to converge to the correct solution. We validate our results against numerical solutions and achieve $99 \%$ accuracy in most scenarios.