A Hybrid Membership Latent Distance Model for Unsigned and Signed Integer Weighted Networks

Graph representation learning (GRL) has become a prominent tool for furthering the understanding of complex networks providing tools for network embedding, link prediction, and node classification. In this paper, we propose the Hybrid Membership-Latent Distance Model (HM-LDM) by exploring how a Latent Distance Model (LDM) can be constrained to a latent simplex. By controlling the edge lengths of the corners of the simplex, the volume of the latent space can be systematically controlled. Thereby communities are revealed as the space becomes more constrained, with hard memberships being recovered as the simplex volume goes to zero. We further explore a recent likelihood formulation for signed networks utilizing the Skellam distribution to account for signed weighted networks and extend the HM-LDM to the signed Hybrid Membership-Latent Distance Model (sHM-LDM). Importantly, the induced likelihood function explicitly attracts nodes with positive links and deters nodes from having negative interactions. We demonstrate the utility of HM-LDM and sHM-LDM on several real networks. We find that the procedures successfully identify prominent distinct structures, as well as how nodes relate to the extracted aspects providing favorable performances in terms of link prediction when compared to prominent baselines. Furthermore, the learned soft memberships enable easily interpretable network visualizations highlighting distinct patterns.

Characterizing Polarization in Social Networks using the Signed Relational Latent Distance Model

Graph representation learning has become a prominent tool for the characterization and understanding of the structure of networks in general and social networks in particular. Typically, these representation learning approaches embed the networks into a low-dimensional space in which the role of each individual can be characterized in terms of their latent position. A major current concern in social networks is the emergence of polarization and filter bubbles promoting a mindset of "us-versus-them" that may be defined by extreme positions believed to ultimately lead to political violence and the erosion of democracy. Such polarized networks are typically characterized in terms of signed links reflecting likes and dislikes. We propose the latent Signed relational Latent dIstance Model (SLIM) utilizing for the first time the Skellam distribution as a likelihood function for signed networks and extend the modeling to the characterization of distinct extreme positions by constraining the embedding space to polytopes. On four real social signed networks of polarization, we demonstrate that the model extracts low-dimensional characterizations that well predict friendships and animosity while providing interpretable visualizations defined by extreme positions when endowing the model with an embedding space restricted to polytopes.

Piecewise-Velocity Model for Learning Continuous-time Dynamic Node Representations

Networks have become indispensable and ubiquitous structures in many fields to model the interactions among different entities, such as friendship in social networks or protein interactions in biological graphs. A major challenge is to understand the structure and dynamics of these systems. Although networks evolve through time, most existing graph representation learning methods target only static networks. Whereas approaches have been developed for the modeling of dynamic networks, there is a lack of efficient continuous time dynamic graph representation learning methods that can provide accurate network characterization and visualization in low dimensions while explicitly accounting for prominent network characteristics such as homophily and transitivity. In this paper, we propose the Piecewise-Velocity Model (PiVeM) for the representation of continuous-time dynamic networks. It learns dynamic embeddings in which the temporal evolution of nodes is approximated by piecewise linear interpolations based on a latent distance model with piecewise constant node-specific velocities. The model allows for analytically tractable expressions of the associated Poisson process likelihood with scalable inference invariant to the number of events. We further impose a scalable Kronecker structured Gaussian Process prior to the dynamics accounting for community structure, temporal smoothness, and disentangled (uncorrelated) latent embedding dimensions optimally learned to characterize the network dynamics. We show that PiVeM can successfully represent network structure and dynamics in ultra-low two-dimensional spaces. It outperforms relevant state-of-art methods in downstream tasks such as link prediction. In summary, PiVeM enables easily interpretable dynamic network visualizations and characterizations that can further improve our understanding of the intrinsic dynamics of time-evolving networks.

A Hierarchical Block Distance Model for Ultra Low-Dimensional Graph Representations

Graph Representation Learning (GRL) has become central for characterizing structures of complex networks and performing tasks such as link prediction, node classification, network reconstruction, and community detection. Whereas numerous generative GRL models have been proposed, many approaches have prohibitive computational requirements hampering large-scale network analysis, fewer are able to explicitly account for structure emerging at multiple scales, and only a few explicitly respect important network properties such as homophily and transitivity. This paper proposes a novel scalable graph representation learning method named the Hierarchical Block Distance Model (HBDM). The HBDM imposes a multiscale block structure akin to stochastic block modeling (SBM) and accounts for homophily and transitivity by accurately approximating the latent distance model (LDM) throughout the inferred hierarchy. The HBDM naturally accommodates unipartite, directed, and bipartite networks whereas the hierarchy is designed to ensure linearithmic time and space complexity enabling the analysis of very large-scale networks. We evaluate the performance of the HBDM on massive networks consisting of millions of nodes. Importantly, we find that the proposed HBDM framework significantly outperforms recent scalable approaches in all considered downstream tasks. Surprisingly, we observe superior performance even imposing ultra-low two-dimensional embeddings facilitating accurate direct and hierarchical-aware network visualization and interpretation.

Topic-aware latent models for representation learning on networks

Network representation learning (NRL) methods have received significant attention over the last years thanks to their success in several graph analysis problems, including node classification, link prediction, and clustering. Such methods aim to map each vertex of the network into a low-dimensional space in a way that the structural information of the network is preserved. Of particular interest are methods based on random walks; such methods transform the network into a collection of node sequences, aiming to learn node representations by predicting the context of each node within the sequence. In this paper, we introduce TNE, a generic framework to enhance the embeddings of nodes acquired by means of random walk-based approaches with topic-based information. Similar to the concept of topical word embeddings in Natural Language Processing, the proposed model first assigns each node to a latent community with the favor of various statistical graph models and community detection methods and then learns the enhanced topic-aware representations. We evaluate our methodology in two downstream tasks: node classification and link prediction. The experimental results demonstrate that by incorporating node and community embeddings, we are able to outperform widely-known baseline NRL models.

${\rm N{\small ode}S{\small ig}}$: Random Walk Diffusion meets Hashing for Scalable Graph Embeddings

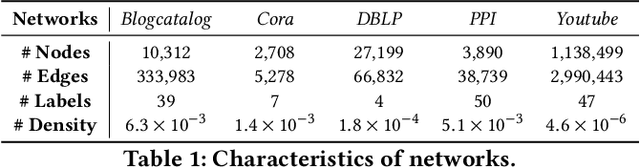
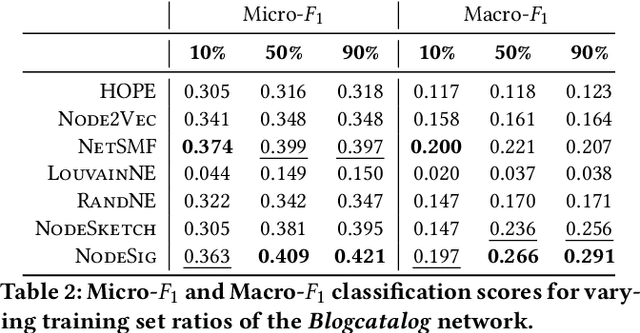
Learning node representations is a crucial task with a plethora of interdisciplinary applications. Nevertheless, as the size of the networks increases, most widely used models face computational challenges to scale to large networks. While there is a recent effort towards designing algorithms that solely deal with scalability issues, most of them behave poorly in terms of accuracy on downstream tasks. In this paper, we aim at studying models that balance the trade-off between efficiency and accuracy. In particular, we propose ${\rm N{\small ode}S{\small ig}}$, a scalable embedding model that computes binary node representations. ${\rm N{\small ode}S{\small ig}}$ exploits random walk diffusion probabilities via stable random projection hashing, towards efficiently computing embeddings in the Hamming space. Our extensive experimental evaluation on various graphs has demonstrated that the proposed model achieves a good balance between accuracy and efficiency compared to well-known baseline models on two downstream tasks.

Exponential Family Graph Embeddings

Representing networks in a low dimensional latent space is a crucial task with many interesting applications in graph learning problems, such as link prediction and node classification. A widely applied network representation learning paradigm is based on the combination of random walks for sampling context nodes and the traditional \textit{Skip-Gram} model to capture center-context node relationships. In this paper, we emphasize on exponential family distributions to capture rich interaction patterns between nodes in random walk sequences. We introduce the generic \textit{exponential family graph embedding} model, that generalizes random walk-based network representation learning techniques to exponential family conditional distributions. We study three particular instances of this model, analyzing their properties and showing their relationship to existing unsupervised learning models. Our experimental evaluation on real-world datasets demonstrates that the proposed techniques outperform well-known baseline methods in two downstream machine learning tasks.

Kernel Node Embeddings

Learning representations of nodes in a low dimensional space is a crucial task with many interesting applications in network analysis, including link prediction and node classification. Two popular approaches for this problem include matrix factorization and random walk-based models. In this paper, we aim to bring together the best of both worlds, towards learning latent node representations. In particular, we propose a weighted matrix factorization model which encodes random walk-based information about the nodes of the graph. The main benefit of this formulation is that it allows to utilize kernel functions on the computation of the embeddings. We perform an empirical evaluation on real-world networks, showing that the proposed model outperforms baseline node embedding algorithms in two downstream machine learning tasks.

TNE: A Latent Model for Representation Learning on Networks

Network representation learning (NRL) methods aim to map each vertex into a low dimensional space by preserving the local and global structure of a given network, and in recent years they have received a significant attention thanks to their success in several challenging problems. Although various approaches have been proposed to compute node embeddings, many successful methods benefit from random walks in order to transform a given network into a collection of sequences of nodes and then they target to learn the representation of nodes by predicting the context of each vertex within the sequence. In this paper, we introduce a general framework to enhance the embeddings of nodes acquired by means of the random walk-based approaches. Similar to the notion of topical word embeddings in NLP, the proposed method assigns each vertex to a topic with the favor of various statistical models and community detection methods, and then generates the enhanced community representations. We evaluate our method on two downstream tasks: node classification and link prediction. The experimental results demonstrate that the incorporation of vertex and topic embeddings outperform widely-known baseline NRL methods.