Dynamic Lambda-Field: A Counterpart of the Bayesian Occupancy Grid for Risk Assessment in Dynamic Environments

In the context of autonomous vehicles, one of the most crucial tasks is to estimate the risk of the undertaken action. While navigating in complex urban environments, the Bayesian occupancy grid is one of the most popular types of map, where the information of occupancy is stored as the probability of collision. Although widely used, this kind of representation is not well suited for risk assessment: because of its discrete nature, the probability of collision becomes dependent on the tessellation size. Therefore, risk assessments on Bayesian occupancy grids cannot yield risks with meaningful physical units. In this article, we propose an alternative framework called Dynamic Lambda-Field that is able to assess physical risks in dynamic environments without being dependent on the tessellation size. Using our framework, we are able to plan safe trajectories where the risk function can be adjusted depending on the scenario. We validate our approach with quantitative experiments, showing the convergence speed of the grid and that the framework is suitable for real-world scenarios.

Lambda-Field: A Continuous Counterpart Of The Bayesian Occupancy Grid For Risk Assessment And Safe Navigation

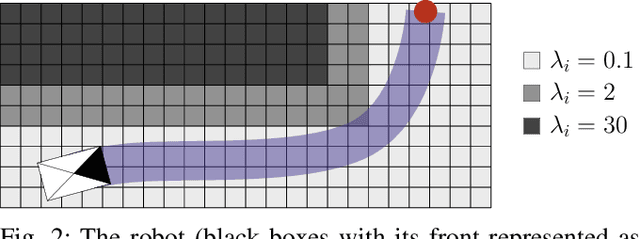
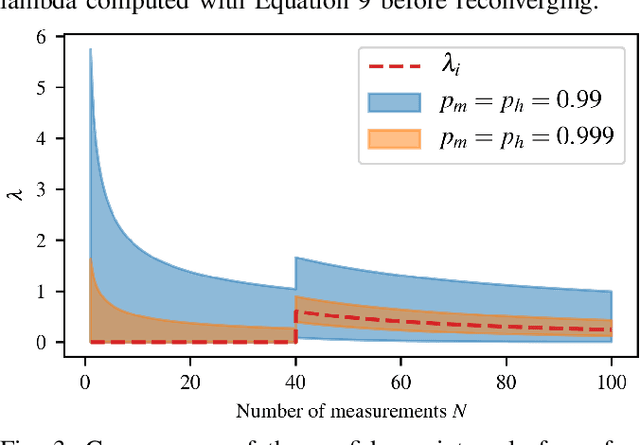
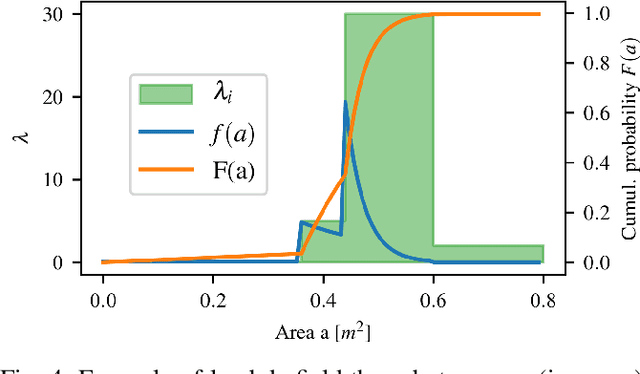
In the context of autonomous robots, one of the most important tasks is to prevent potential damages on the robot during navigation. For this purpose, it is often assumed to deal with known probabilistic obstacles, then to compute the probability of collision to each obstacle. However, in complex scenarios or unstructured environments, it might be difficult to detect such obstacles. In this case, a metric map is used where each position stores the information of occupancy. The most common type of metric map is the bayesian occupancy map. However, this type of map is not well fitted to compute risk assessment for continuous paths due to its discrete nature. Hence, we introduce a novel type of map called Lambda-Field, specially designed for risk assessment. We first propose a way to compute such a map and the expectancy of a generic risk over a path. Then, we demonstrate the utility of our generic formulation with a use case defining the risk as the expected force of collision over a path. Using this risk definition and the Lambda-Field, we show that our framework is capable of doing classical path planning while having a physical-based metric. Furthermore, the Lambda-Field gives a natural way to deal with unstructured environments like tall grass. Where standard environment representations would generate trajectories going around such obstacles, our framework allows the robot to go through the grass while being aware of the risk taken.