Zeroth-Order Algorithms for Nonconvex Minimax Problems with Improved Complexities

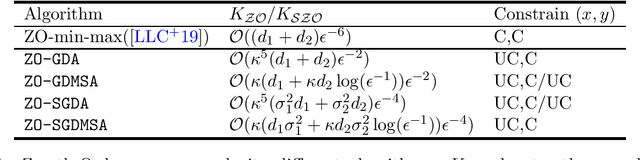
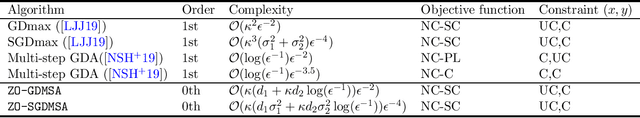
In this paper, we study zeroth-order algorithms for minimax optimization problems that are nonconvex in one variable and strongly-concave in the other variable. Such minimax optimization problems have attracted significant attention lately due to their applications in modern machine learning tasks. We first design and analyze the Zeroth-Order Gradient Descent Ascent (\texttt{ZO-GDA}) algorithm, and provide improved results compared to existing works, in terms of oracle complexity. Next, we propose the Zeroth-Order Gradient Descent Multi-Step Ascent (\texttt{ZO-GDMSA}) algorithm that significantly improves the oracle complexity of \texttt{ZO-GDA}. We also provide stochastic version of \texttt{ZO-GDA} and \texttt{ZO-GDMSA} to handle stochastic nonconvex minimax problems, and provide oracle complexity results.