XAI for Graphs: Explaining Graph Neural Network Predictions by Identifying Relevant Walks
Paper and Code
Jun 12, 2020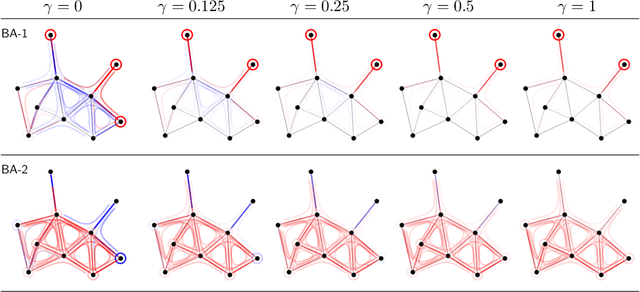
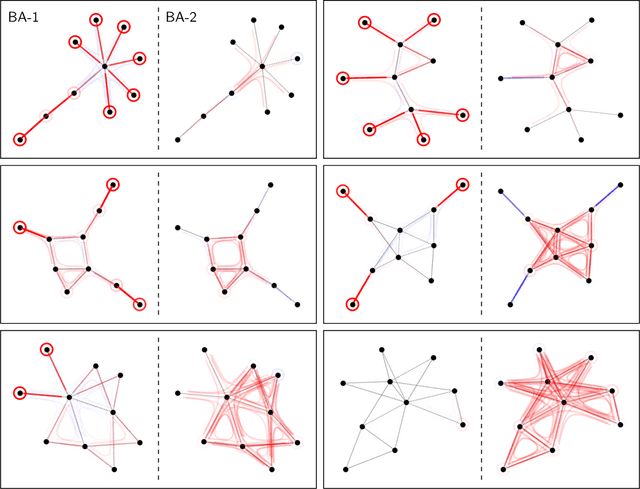
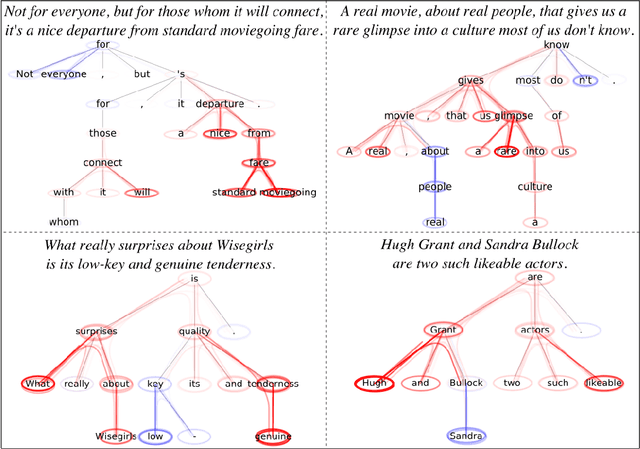
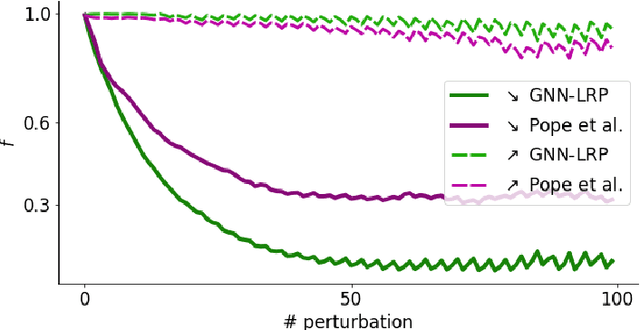
Graph Neural Networks (GNNs) are a popular approach for predicting graph structured data. As GNNs tightly entangle the input graph into the neural network structure, common explainable AI (XAI) approaches are not applicable. To a large extent, GNNs have remained black-boxes for the user so far. In this paper, we contribute by proposing a new XAI approach for GNNs. Our approach is derived from high-order Taylor expansions and is able to generate a decomposition of the GNN prediction as a collection of relevant walks on the input graph. We find that these high-order Taylor expansions can be equivalently (and more simply) computed using multiple backpropagation passes from the top layer of the GNN to the first layer. The explanation can then be further robustified and generalized by using layer-wise-relevance propagation (LRP) in place of the standard equations for gradient propagation. Our novel method which we denote as 'GNN-LRP' is tested on scale-free graphs, sentence parsing trees, molecular graphs, and pixel lattices representing images. In each case, it performs stably and accurately, and delivers interesting and novel application insights.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge