WrapNet: Neural Net Inference with Ultra-Low-Resolution Arithmetic
Paper and Code
Jul 26, 2020
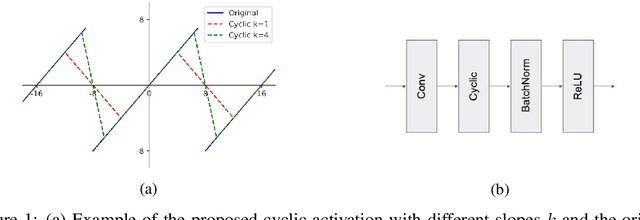

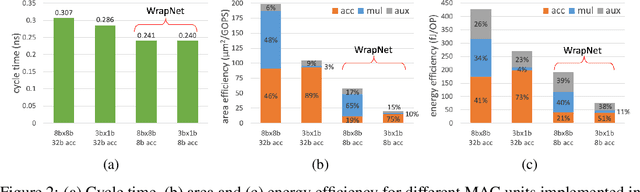
Low-resolution neural networks represent both weights and activations with few bits, drastically reducing the multiplication complexity. Nonetheless, these products are accumulated using high-resolution (typically 32-bit) additions, an operation that dominates the arithmetic complexity of inference when using extreme quantization (e.g., binary weights). To further optimize inference, we propose a method that adapts neural networks to use low-resolution (8-bit) additions in the accumulators, achieving classification accuracy comparable to their 32-bit counterparts. We achieve resilience to low-resolution accumulation by inserting a cyclic activation layer, as well as an overflow penalty regularizer. We demonstrate the efficacy of our approach on both software and hardware platforms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge