Widely Linear Kernels for Complex-Valued Kernel Activation Functions
Paper and Code
Feb 06, 2019
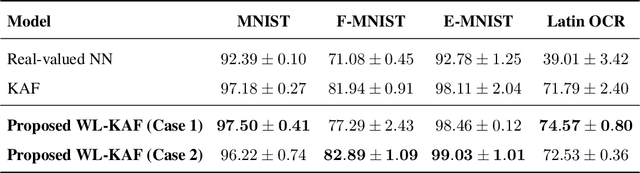
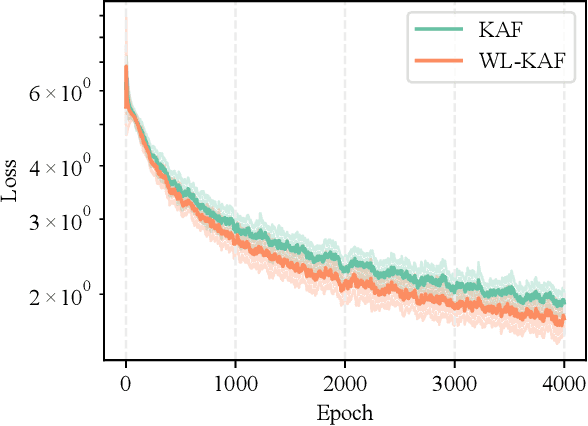
Complex-valued neural networks (CVNNs) have been shown to be powerful nonlinear approximators when the input data can be properly modeled in the complex domain. One of the major challenges in scaling up CVNNs in practice is the design of complex activation functions. Recently, we proposed a novel framework for learning these activation functions neuron-wise in a data-dependent fashion, based on a cheap one-dimensional kernel expansion and the idea of kernel activation functions (KAFs). In this paper we argue that, despite its flexibility, this framework is still limited in the class of functions that can be modeled in the complex domain. We leverage the idea of widely linear complex kernels to extend the formulation, allowing for a richer expressiveness without an increase in the number of adaptable parameters. We test the resulting model on a set of complex-valued image classification benchmarks. Experimental results show that the resulting CVNNs can achieve higher accuracy while at the same time converging faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge