Why Train More? Effective and Efficient Membership Inference via Memorization
Paper and Code
Oct 12, 2023
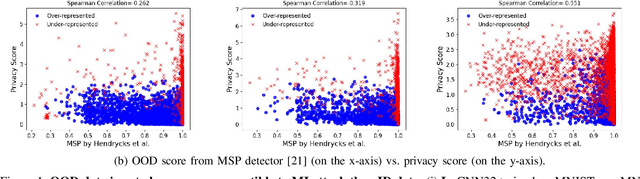
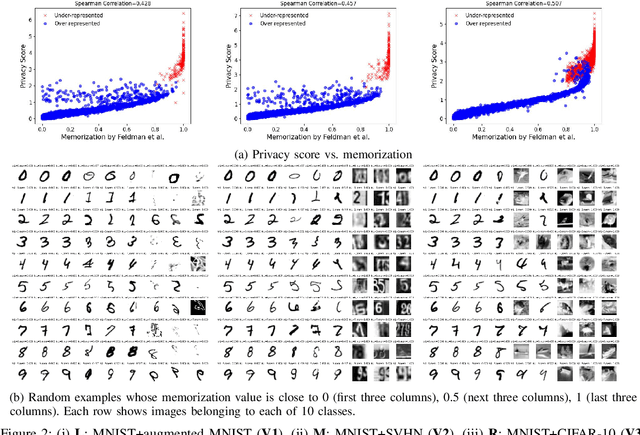
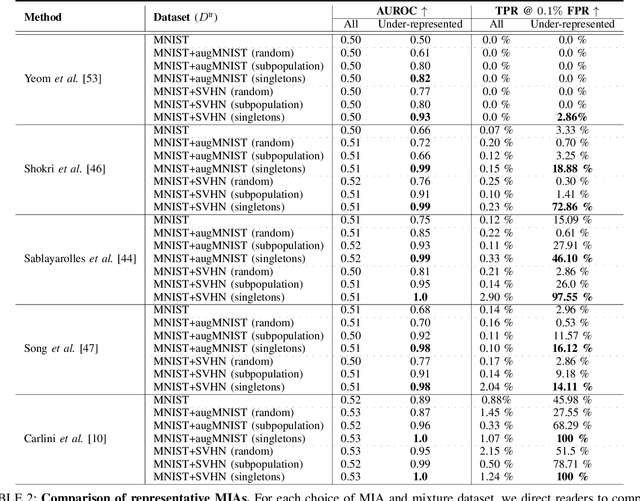
Membership Inference Attacks (MIAs) aim to identify specific data samples within the private training dataset of machine learning models, leading to serious privacy violations and other sophisticated threats. Many practical black-box MIAs require query access to the data distribution (the same distribution where the private data is drawn) to train shadow models. By doing so, the adversary obtains models trained "with" or "without" samples drawn from the distribution, and analyzes the characteristics of the samples under consideration. The adversary is often required to train more than hundreds of shadow models to extract the signals needed for MIAs; this becomes the computational overhead of MIAs. In this paper, we propose that by strategically choosing the samples, MI adversaries can maximize their attack success while minimizing the number of shadow models. First, our motivational experiments suggest memorization as the key property explaining disparate sample vulnerability to MIAs. We formalize this through a theoretical bound that connects MI advantage with memorization. Second, we show sample complexity bounds that connect the number of shadow models needed for MIAs with memorization. Lastly, we confirm our theoretical arguments with comprehensive experiments; by utilizing samples with high memorization scores, the adversary can (a) significantly improve its efficacy regardless of the MIA used, and (b) reduce the number of shadow models by nearly two orders of magnitude compared to state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge