Who is Afraid of Big Bad Minima? Analysis of Gradient-Flow in a Spiked Matrix-Tensor Model
Paper and Code
Jul 22, 2019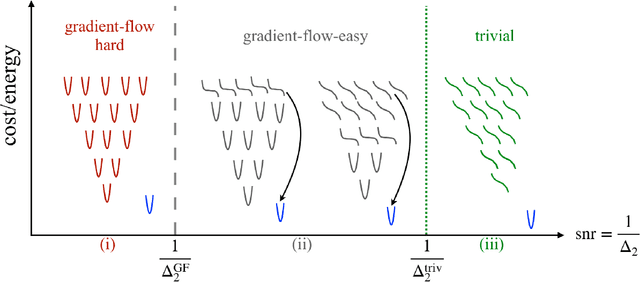
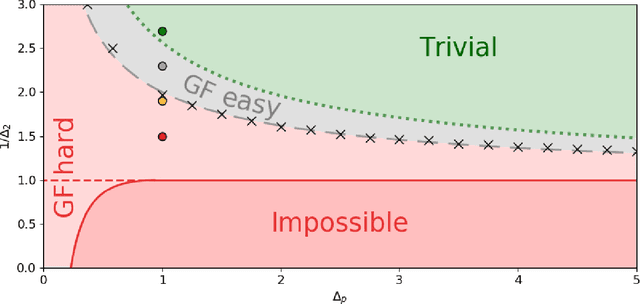
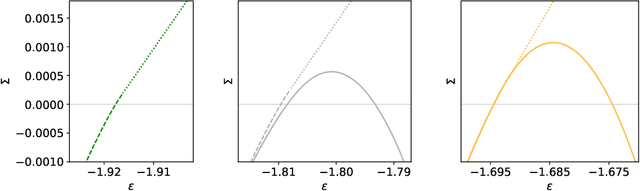
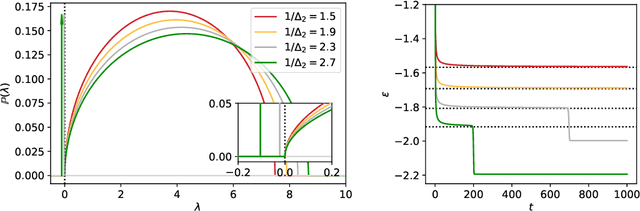
Gradient-based algorithms are effective for many machine learning tasks, but despite ample recent effort and some progress, it often remains unclear why they work in practice in optimising high-dimensional non-convex functions and why they find good minima instead of being trapped in spurious ones. Here we present a quantitative theory explaining this behaviour in a spiked matrix-tensor model. Our framework is based on the Kac-Rice analysis of stationary points and a closed-form analysis of gradient-flow originating from statistical physics. We show that there is a well defined region of parameters where the gradient-flow algorithm finds a good global minimum despite the presence of exponentially many spurious local minima. We show that this is achieved by surfing on saddles that have strong negative direction towards the global minima, a phenomenon that is connected to a BBP-type threshold in the Hessian describing the critical points of the landscapes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge