Waveformer: Linear-Time Attention with Forward and Backward Wavelet Transform

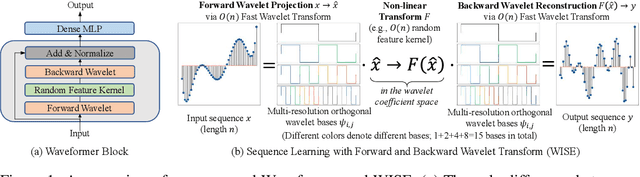
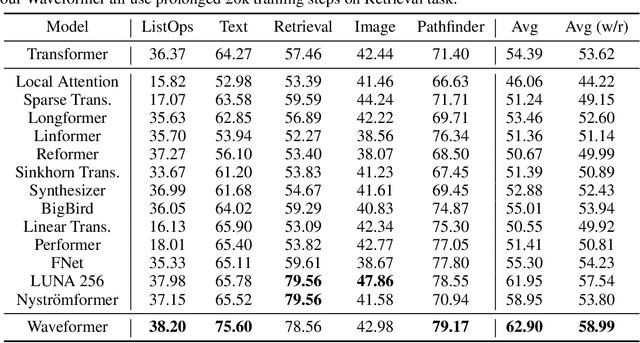
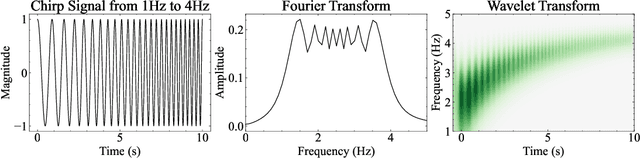
We propose Waveformer that learns attention mechanism in the wavelet coefficient space, requires only linear time complexity, and enjoys universal approximating power. Specifically, we first apply forward wavelet transform to project the input sequences to multi-resolution orthogonal wavelet bases, then conduct nonlinear transformations (in this case, a random feature kernel) in the wavelet coefficient space, and finally reconstruct the representation in input space via backward wavelet transform. We note that other non-linear transformations may be used, hence we name the learning paradigm Wavelet transformatIon for Sequence lEarning (WISE). We emphasize the importance of backward reconstruction in the WISE paradigm -- without it, one would be mixing information from both the input space and coefficient space through skip connections, which shall not be considered as mathematically sound. Compared with Fourier transform in recent works, wavelet transform is more efficient in time complexity and better captures local and positional information; we further support this through our ablation studies. Extensive experiments on seven long-range understanding datasets from the Long Range Arena benchmark and code understanding tasks demonstrate that (1) Waveformer achieves competitive and even better accuracy than a number of state-of-the-art Transformer variants and (2) WISE can boost accuracies of various attention approximation methods without increasing the time complexity. These together showcase the superiority of learning attention in a wavelet coefficient space over the input space.