Wasserstein-Wasserstein Auto-Encoders
Paper and Code
Feb 25, 2019
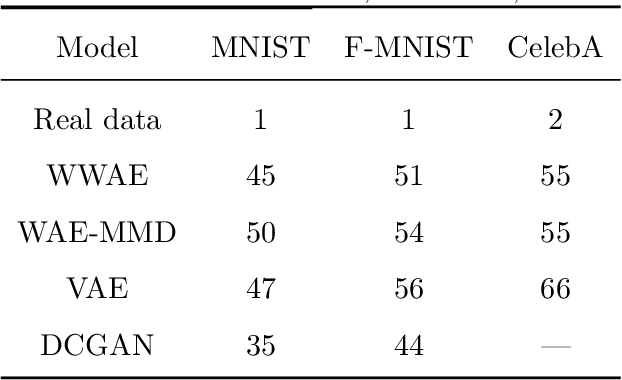


To address the challenges in learning deep generative models (e.g.,the blurriness of variational auto-encoder and the instability of training generative adversarial networks, we propose a novel deep generative model, named Wasserstein-Wasserstein auto-encoders (WWAE). We formulate WWAE as minimization of the penalized optimal transport between the target distribution and the generated distribution. By noticing that both the prior $P_Z$ and the aggregated posterior $Q_Z$ of the latent code Z can be well captured by Gaussians, the proposed WWAE utilizes the closed-form of the squared Wasserstein-2 distance for two Gaussians in the optimization process. As a result, WWAE does not suffer from the sampling burden and it is computationally efficient by leveraging the reparameterization trick. Numerical results evaluated on multiple benchmark datasets including MNIST, fashion- MNIST and CelebA show that WWAE learns better latent structures than VAEs and generates samples of better visual quality and higher FID scores than VAEs and GANs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge