Visual Processing by a Unified Schatten-$p$ Norm and $\ell_q$ Norm Regularized Principal Component Pursuit
Paper and Code
Aug 20, 2016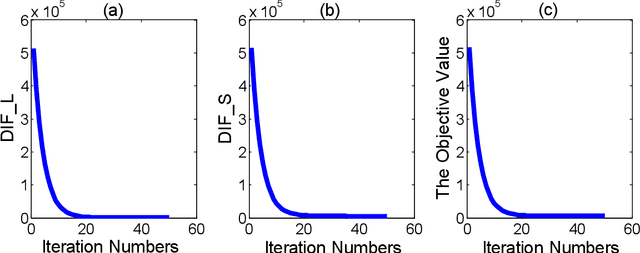
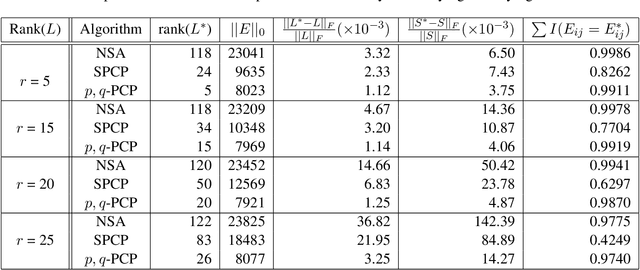
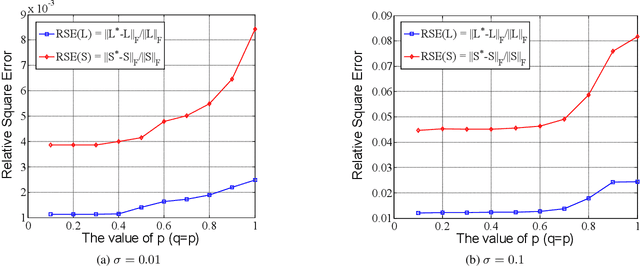
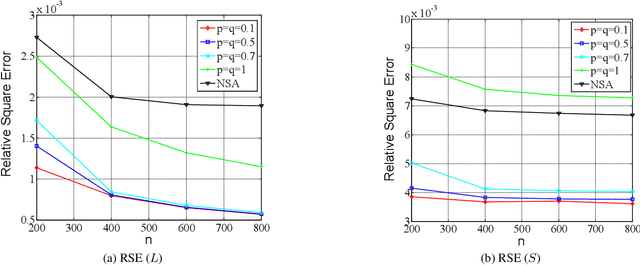
In this paper, we propose a non-convex formulation to recover the authentic structure from the corrupted real data. Typically, the specific structure is assumed to be low rank, which holds for a wide range of data, such as images and videos. Meanwhile, the corruption is assumed to be sparse. In the literature, such a problem is known as Robust Principal Component Analysis (RPCA), which usually recovers the low rank structure by approximating the rank function with a nuclear norm and penalizing the error by an $\ell_1$-norm. Although RPCA is a convex formulation and can be solved effectively, the introduced norms are not tight approximations, which may cause the solution to deviate from the authentic one. Therefore, we consider here a non-convex relaxation, consisting of a Schatten-$p$ norm and an $\ell_q$-norm that promote low rank and sparsity respectively. We derive a proximal iteratively reweighted algorithm (PIRA) to solve the problem. Our algorithm is based on an alternating direction method of multipliers, where in each iteration we linearize the underlying objective function that allows us to have a closed form solution. We demonstrate that solutions produced by the linearized approximation always converge and have a tighter approximation than the convex counterpart. Experimental results on benchmarks show encouraging results of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge